Note: please find the 2022's note here.
This is a note page in which I have collected my interested arXiv preprints (gr-qc) and ranked in time. All the figures are credited to the corresponding paper linked above them.
Please click here to refresh the page if the formulas are not rendered.
March
3-10
Searching for ultralight bosons with spin measurements of a population of binary black hole mergers
- The paper shows that hundreds of high SNR GW events should be considered in a hierarchical Bayesian inference method to exclude (confirm) the existence of noninteracting bosons in one mass range due to the large uncertainty of current ground-based GW detectors.
- Ultralight bosons can form clouds around rotating black holes if their Compton wavelength is comparable to the black hole size. The boson cloud spins down the black hole through a process called superradiance, lowering the black hole spin to a characteristic spin determined by the boson mass and the black hole mass. It has been suggested that spin measurements of the black holes detected by ground-based gravitational-wave detectors can be used to constrain the mass of ultralight bosons. Unfortunately, a measurement of the individual black hole spins is often uncertain, resulting in inconclusive results.
May
5-26
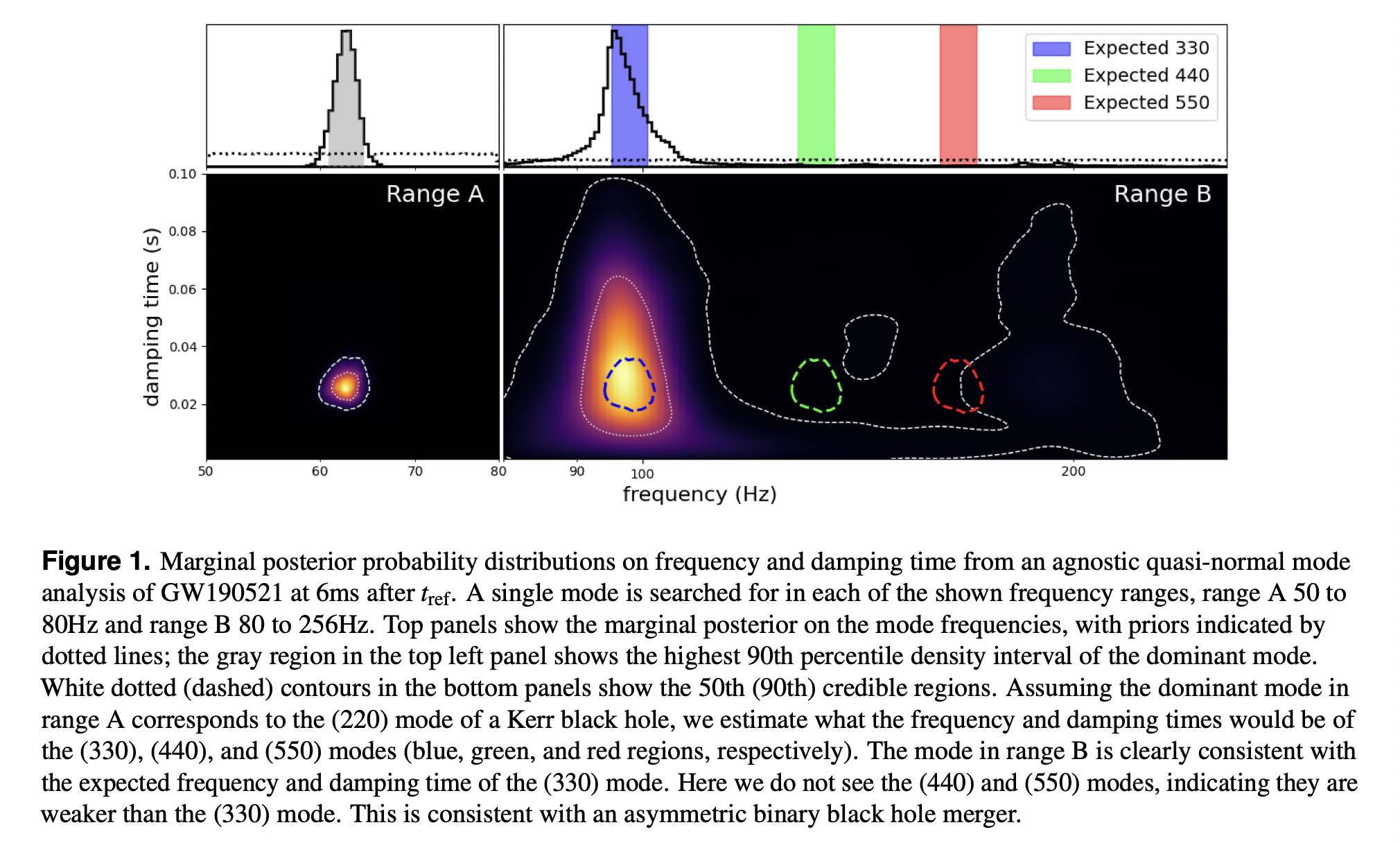
Observation of a multimode quasi-normal spectrum from a perturbed black hole
- Using GW190521, a Bayes factor of \(\sim 40\) preferring two fundamental modes (the dominant \(\ell=m=2\) harmonic, and the sub-dominant mode corresponds to the \(\ell=m=3\) harmonic). The results highlight the benefits of black hole spectroscopy using the fundamental modes since overtones are poorly constraint.
June
6-17
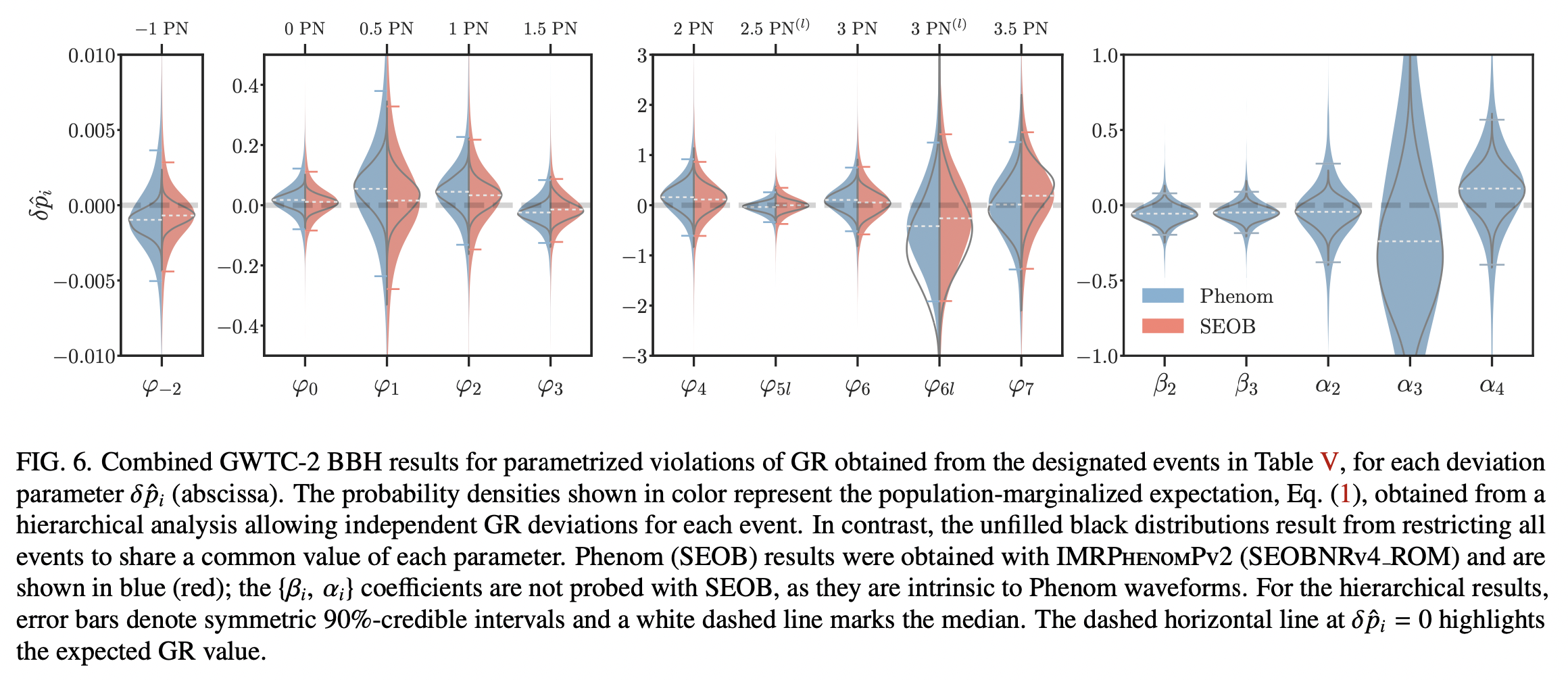
Tests of General Relativity with Binary Black Holes from the second LIGO–Virgo Gravitational-Wave Transient Catalog
- Testing several aspects of possible deviation from GR via examine the consistency between the theoretically prediceted parameterized modification to GW waveform and the data, while giving more stringent constraints on the deviation parameters space. To understand our measurements holistically, a variety of statistical techniques are used, including hierarchical Bayesian inference.
- Conclusions:
- Confirmed that events return compatible parameter estimates when the low- and high-frequency regimes are analyzed separately.
- Improved previous constraints by a factor of ∼2 in testing deviations away from the GR prediction for the GW waveform via allowing for corrections to the GW phasing through inspiral PN parameters, as well as phenomenological merger-ringdown coefficients.
- The population-marginalized constraint on the fractional deviation away from the Kerr spectrum frequency is \(\delta \hat{f}_{220}=0.03_{-0.35}^{+0.38}\) for the 220 mode, and \(\delta \hat{f}_{221}=0.04_{-0.32}^{+0.27}\) for the 221 mode at \(90 \%\) credibility. No significant evidence for GW echoes.
- With only three active detectors, it's impossible to simultaneously constrain all the six possible GW polarizations allowed in generic metric theories of gravity (scalar, vector, and tensor). Instead, as in previous studies, the likelihood of having purely scalar or purely vector polarizations are compared against the pure tensor case, pre- dicted by GR. We found no evidence in favor of non-tensor GWs.
6-21
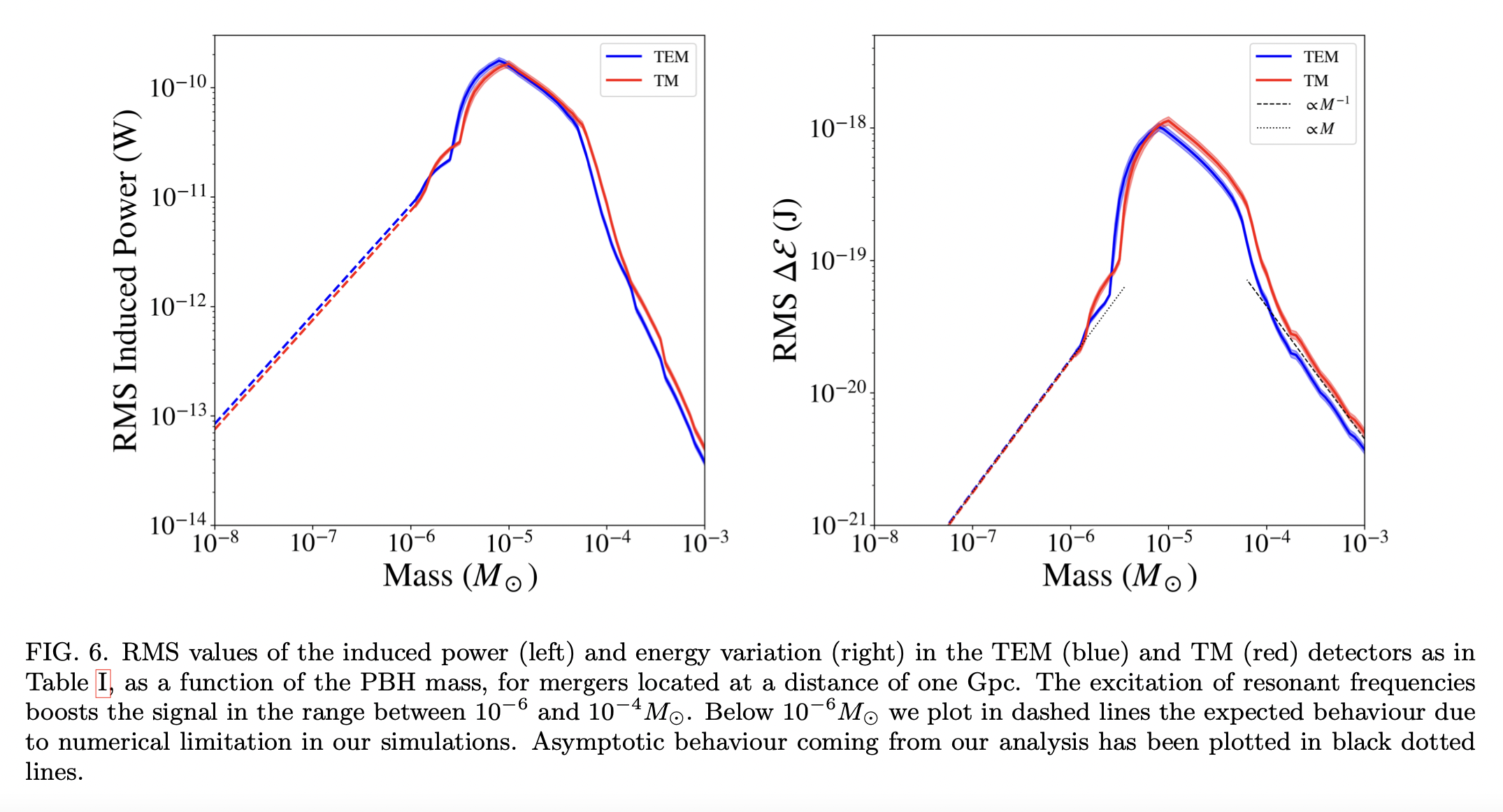
Detecting Planetary-mass Primordial Black Holes with Resonant Electromagnetic Gravitational Wave Detectors
Considerring the possibility of detecting PBH binary mergers of mass around \(10^{−5}M_⊙\) with two patented experimental designs based on the inverse Gertsenshtein effect.
The Einstein-Maxwell system models the interplay of gravitation and electromagnetism by the coupling of their respective field equations: \[ \begin{aligned} R_{\mu \nu} &=\frac{8 \pi G}{c^{4}} T_{\mu \nu}^{(\mathrm{em})} \\ \nabla_{\mu} F^{\mu \nu} &=-\mu_{0} J^{\nu} \end{aligned} \] where: \[ T_{\mu \nu}^{(\mathrm{em})}=\frac{1}{\mu_{0}}\left(g^{\alpha \beta} F_{\mu \alpha} F_{\nu \beta}-\frac{1}{4} g_{\mu \nu} F_{\alpha \beta} F^{\alpha \beta}\right) \] is the Maxwell stress-energy tensor, \(F_{\mu \nu}=\partial_{\mu} A_{\nu}-\partial_{\nu} A_{\mu}\) being the Faraday tensor of the electromagnetic field, \(g_{\mu \nu}\) and \(A_{\mu}\) are the metric and the four-vector potential.
Indeed, the metric perturbations \(h_{\mu \nu}\) produced through the Gerstenshtein mechanism (a wave resonance mechanism in which light passing through a region of uniform magnetic field, perpendicular to the direction of light propagation, produces GWs) have an amplitude of order: \[ h_{\mu \nu} \sim \frac{4 G B_{0} E_{0} L^{2}}{c^{5} \mu_{0}} \] where \(L\) is the size of the region in which the magnetic field and the EM wave interact, and where \(B_{0}\) and \(E_{0}\) are the amplitudes of the static magnetic and varying electric fields respectivelv. \(h_{\mu \nu}\) denotes the gravitational wave generated by the coupling between the external static field \(F_{\mu \nu}^{(s)}\) and some \(\mathrm{EM}\) wave \(F_{\mu \nu}^{(v)}\).
July
7-9
LIGO Detector Characterization in the Second and Third Observing Runs
- LIGO data contains a high rate of transient noise artifacts, or glitches.
- The central signal processing and data visualization engine used to prepare most figures in this paper is GWpy.
7-19
Hairy Black Holes from Horndeski Theory
Extension of the work which derive the static, spherically symmetry BH solution in Horndeski theory by calculate the Hawking temperature (\(T_{H}=\frac{1+Q}{8 \pi G M}\)) and BH geometrical entropy (\(S_{\text {geom }}=\frac{1}{4(1+Q)} A_{\text {out }}\)) with comparison to those in Schwarzschild BH.
The cosmological constant in GR poses an sinsurmountable problem to QFT since it can't agree with the vacuum energy calculation (Weinberg, 1989).
Horndeski theory and beyond see review from here.
In Horndeski theory: \[ \begin{aligned} S &=\int \sqrt{-g} d^{4} x\left(\mathcal{L}_{2}+\mathcal{L}_{3}+\mathcal{L}_{4}+\mathcal{L}_{5}+\mathcal{L}_{4}^{\mathrm{bH}}+\mathcal{L}_{5}^{\mathrm{bH}}\right) \\ \mathcal{L}_{2}=& G_{2}(X) \\ \mathcal{L}_{3}=&-G_{3}(X) \square \phi \\ \mathcal{L}_{4}=& G_{4}(X) R+G_{4 X}\left[(\square \phi)^{2}-\left(\nabla_{\mu} \nabla_{\nu} \phi\right)^{2}\right] \\ \mathcal{L}_{5}=& G_{5}(X) G_{\mu \nu} \nabla^{\mu} \nabla^{\nu} \phi-\frac{1}{6} G_{5 X}\left[(\square \phi)^{3}-3 \square \phi\left(\nabla_{\mu} \nabla_{\nu} \phi\right)^{2}\right.\\ &\left.\quad+2\left(\nabla_{\mu} \nabla_{\nu} \phi\right)^{3}\right] \\ \mathcal{L}_{4}^{\mathrm{bH}}=& F_{4}(X) \epsilon^{\mu \nu \rho \sigma} \epsilon^{\alpha \beta \gamma} \sigma_{\mu} \phi \nabla_{\alpha} \phi \nabla_{\nu} \nabla_{\beta} \phi \nabla_{\rho} \nabla_{\gamma} \phi, \\ \mathcal{L}_{5}^{\mathrm{bH}}=& F_{5}(X) \epsilon^{\mu \nu \rho \sigma} \epsilon^{\alpha \beta \gamma \delta} \nabla_{\mu} \phi \nabla_{\alpha} \phi \nabla_{\nu} \nabla_{\beta} \phi \nabla_{\rho} \nabla_{\gamma} \phi \nabla_{\sigma} \nabla_{\delta} \phi, \end{aligned} \]
\(G_2, G_3, G_4, G_5\) are denoted for ordinary Horndeski, as well as \(F_4\) and \(F_5\) for beyond. The kinetic term \(\chi=-g^{\mu \nu} \phi_{,\mu} \phi_{,\nu} / 2\).
For the static and spherically symmetry BH solution, there exist a choice of these function (see this paper): \[ \begin{array}{l} G_{2} \supseteq \sqrt{-X} \\ G_{3} \supseteq \ln |X| \\ G_{4} \supseteq \sqrt{-X} \\ G_{5} \supseteq \ln |X| \\ F_{4} \supseteq(-X)^{-3 / 2} \\ F_{5} \supseteq X^{-2} \end{array} \] And in this work, where the Horndeski terms are limited to quadratic, the author uses a parameterized choice: \[ \begin{aligned} Q_{2} &=\alpha_{21} \chi+\alpha_{22}(-\chi)^{\omega_{2}} \\ Q_{3} &=\alpha_{31}(-\chi)^{\omega_{3}} \\ Q_{4} &=\kappa^{-2}+\alpha_{42}(-\chi)^{\omega_{4}} \end{aligned} \] the factor (hair) that will be used is \(Q=q/2GM\), and: \[ q \equiv\left(\frac{2}{3}\right)^{3 / 2} \kappa^{2} \alpha_{42} \sqrt{-\frac{\alpha_{42}}{\alpha_{22}}} \] and \(\alpha_{21}=\alpha_{31}=0, \quad \omega_{2}=\frac{3}{2}, \quad \omega_{4}=\frac{1}{2}\) were also constraint by the condition.
7-20
Pseudospectrum of Reissner-Nordström black holes: quasinormal mode instability and universality
Using a hyperboloidal approach to BH perturbation, present the pseudospectrum of scalar and gravitoelectric perturbations in the RN spacetime, and show that for all values of the BH charge \(Q/M ∈ [0,1]\) and for all perturbing fields: they are all similar to typically spectrally unstable systems, which have logarithmic asymptotic behavior in the large-frequency regime.
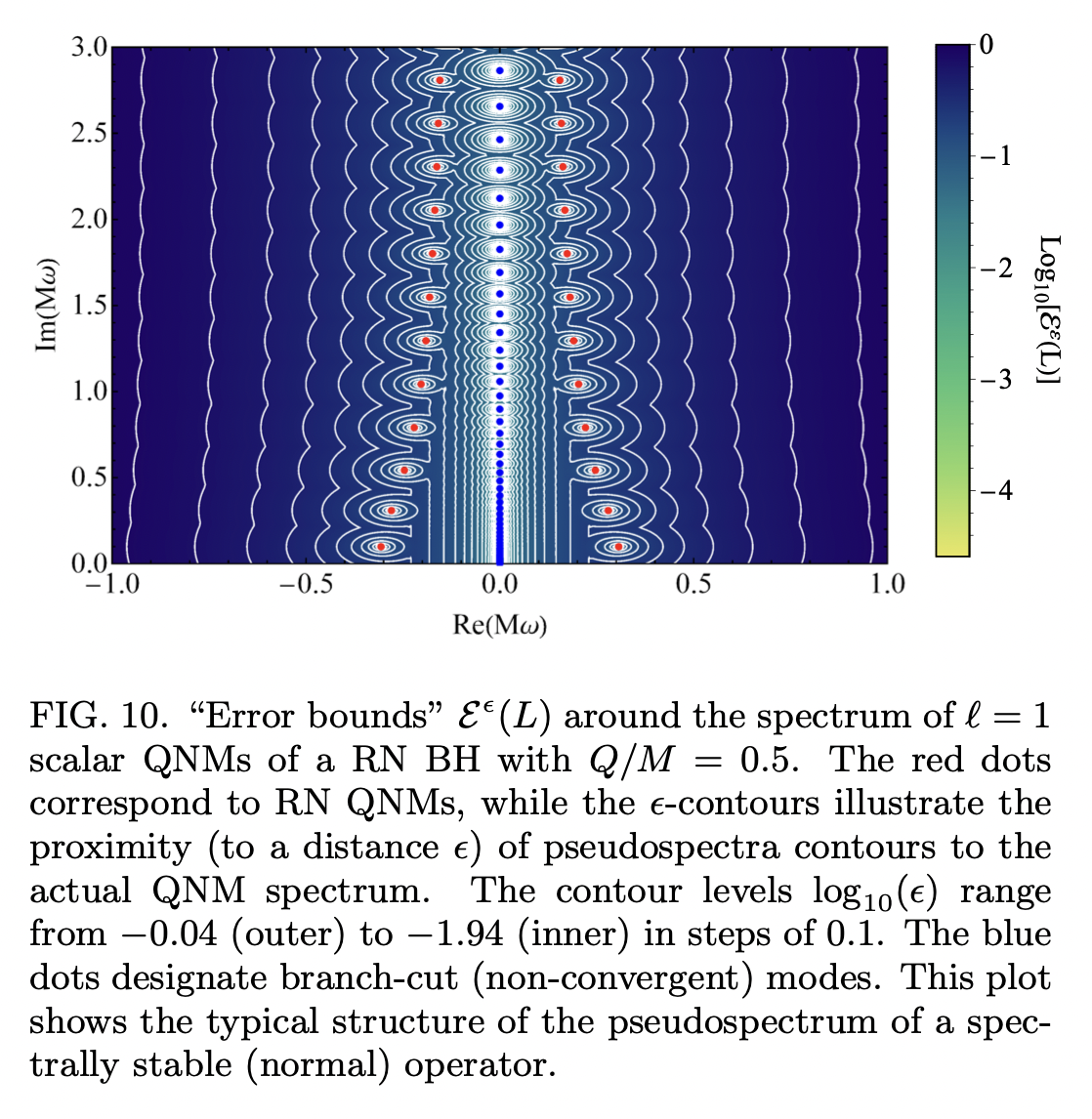
Implement Chebyshev spectral methods to numerically calculate the pseudospectrum. \[ \langle u, v\rangle_{E}=\left(u^{*}\right)^{i} G_{i j}^{E} v^{j}=u^{*} \cdot G^{E} \cdot v, \quad u, v \in \mathbb{C}^{\mathcal{N}}, \] above is the Chebyshev-discretized version of the energy scalar product norm (details see Appendix A of Ref).
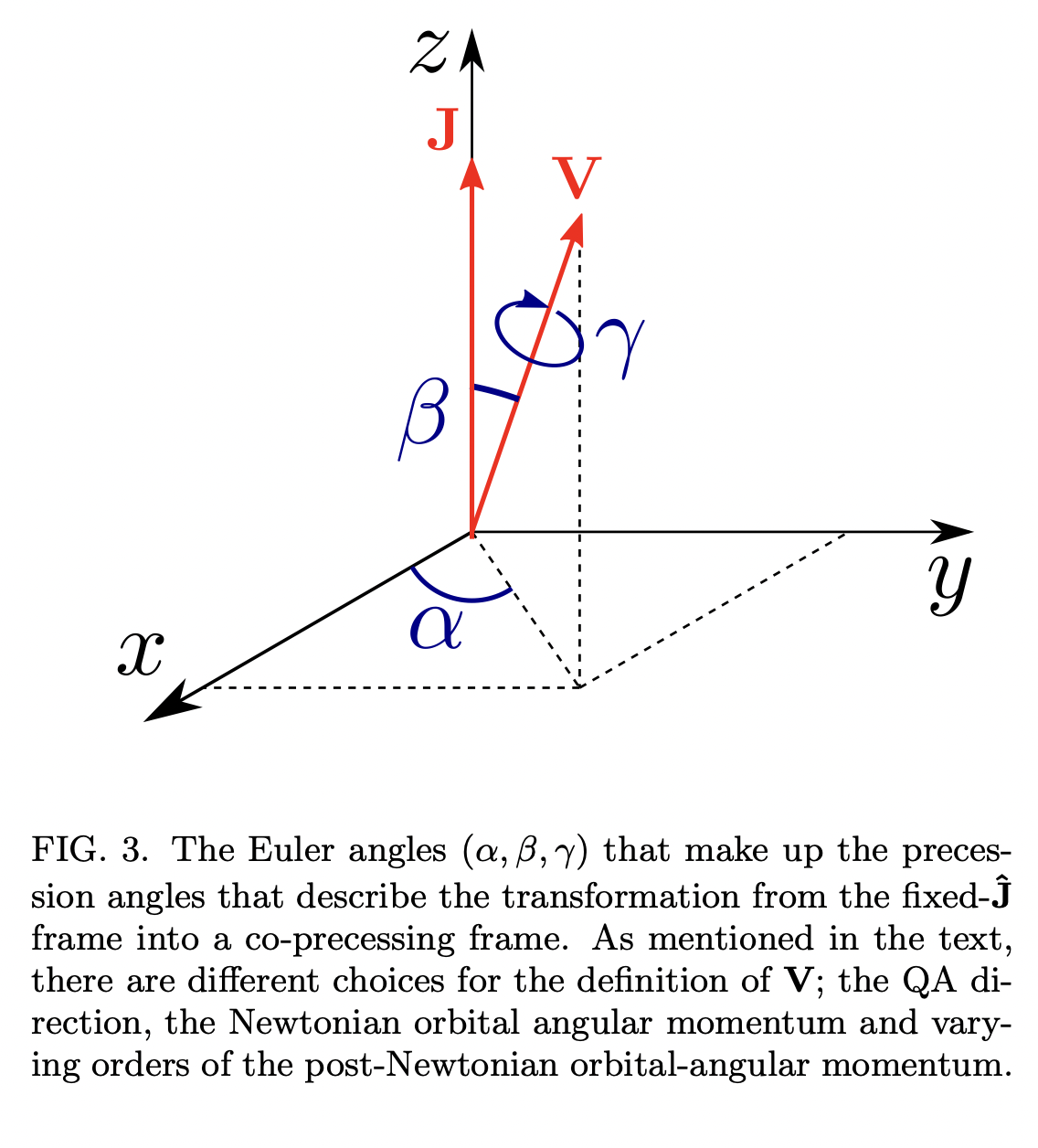
The final twist: A model of gravitational waves from precessing black-hole binaries through merger and ringdown
Provide the first PhenomPNR waveform that can describe the precessing (aligned-spin) BBH system.
From a set of spin-weighted spherical-harmonic multipoles \(q_{\ell m^{\prime}}^{1}\) , if we rotate the coordinate system through the Euler angles (α, β, γ), then the multipoles in the new frame \(q_{\ell m}^{2}\) are given by: \[ q_{\ell m}^{2}=\sum_{m^{\prime}=-\ell}^{\ell} e^{i m^{\prime} \alpha} d_{m^{\prime} m}^{\ell}(-\beta) e^{i m \gamma} q_{\ell m^{\prime}}^{1} \]
Black-Hole Neutron Star Simulations with the BAM code: First Tests and Simulations
BAM code first test on NS-BH (observation GW200105, GW200115) simulation. Previous code includes:
- Spells code of SXS collaboration.
- TwoPunctures code
- LORENE code
- FUKA code
The codes run in a Z4 formalism: \[ \begin{aligned} R_{\alpha \beta}+\nabla_{\alpha} Z_{\beta} &+\nabla_{\beta} Z_{\alpha}=8 \pi\left(T_{\alpha \beta}-\frac{1}{2} g_{\alpha \beta} T\right) \\ &+\kappa_{1}\left(t_{\alpha} Z_{\beta}+t_{\beta} Z_{\alpha}-\left(1+\kappa_{2}\right) g_{\alpha \beta}\right) t_{\gamma} Z^{\gamma} \end{aligned} \] where the \(Z_\alpha\) is a four-vector consisting of constraints, \(t_\alpha\) is a timelike vector, and \(\kappa_1, \kappa_2\) are damping parameters.
One of the author Tim Dietrich is in AEI Potsdam.
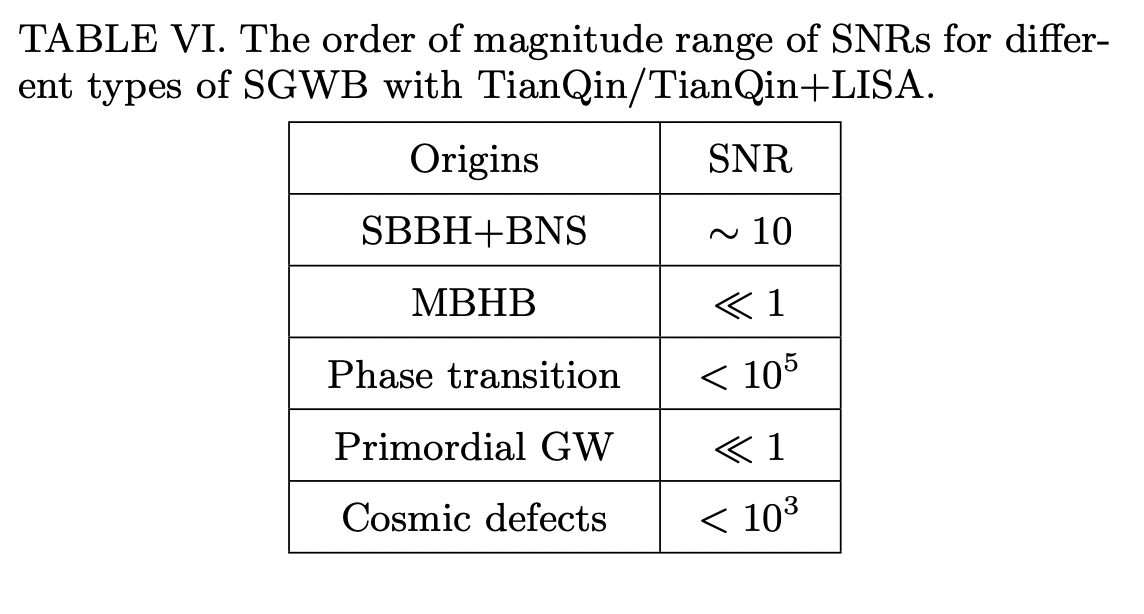
Science with the TianQin Observatory: Preliminary Results on Stochastic Gravitational-Wave Background
Investigate the detectability of TianQin (+LISA) about the stochastic GWs using both cross-correlation and null channel.
For the space GW detections, the laser phase noise is usually orders of magnitude higher than other noises, while the time delay interferometer (TDI) can beat down such noise well.
7-21
Testing waveform models using angular momentum
Use the angular momentum balnace law, check the consistency from PN form. inital spin to flux model fitting final spin. Also this paper may be useful for precessing systems analysis of Phenom. models.
The angular momentum balance law: \[ J^{k}\left(t_{f}\right)=J^{k}\left(t_{i}\right)+\mathcal{F}^{k} \] and the flux \(\mathcal{F}^{k}\): \[ \mathcal{F}^{k}=\frac{i}{32 \pi} \int_{t_{i}}^{t_{f}} \mathrm{~d} t \mathrm{~d} \Omega \overline{\mathrm{O}} \hat{r}^{k}\left(\dot{h}^{\circ} \mathrm{O} \bar{h}^{\circ}+\dot{\bar{h}}^{\circ} \mathfrak{\partial} h^{\circ}-2 \AA\left(\dot{h}^{\circ} \bar{h}^{\circ}\right)\right)+c.c. \] where \(h^{\circ}=r h=r\left(h_{+}-i h_{\times}\right)\) and \(r\) is the luminosity distance.
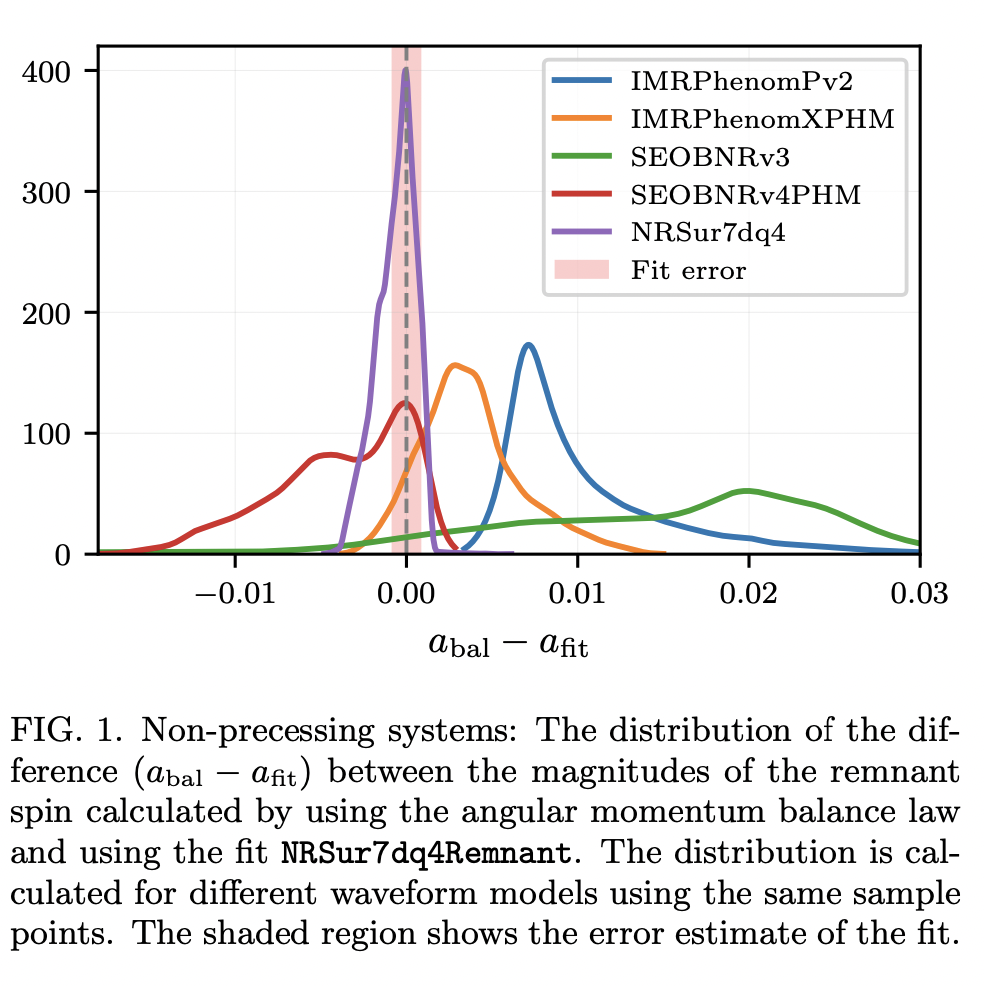
7-22
GWsim: a code to simulate gravitational waves propagating in a potential well
Using finite element method to simulate the propagation of GWs (time domain) in a potential well. The author Jianhua He is from Nanjing University.
\(\Omega \subset \mathbb{R}^{3}\) is a space with boundary \(\partial \Omega\). The boundary value problem (BVP) can be presented as: \[ c^{2} \nabla^{2} u-\frac{\partial^{2}}{\partial t^{2}} u=c^{2} f \quad \text { in } \quad \Omega \times(0, T] \] together with the initial and boundary conditions, are called the strong formulation.
Multiply Eq. (10) by a test function \(\phi\) and then integrate over \(\Omega\), we will obtain a variational equation: \[ \begin{aligned} &-\int_{\Omega} \nabla u \cdot \nabla\left(c^{2} \phi\right) \mathrm{d} x+\int_{\partial \Omega}(\hat{n} \cdot \nabla u)\left(c^{2} \phi\right) \mathrm{d} x-\frac{\partial^{2}}{\partial t^{2}} \int_{\Omega} u \phi \mathrm{d} x \\ =& \int_{\Omega} c^{2} f \phi \mathrm{d} x \quad \forall \phi \in V \end{aligned} \] where we have used the Green's formula: \[ \int_{\Omega} c^{2} \phi \nabla^{2} u \mathrm{~d} x=-\int_{\Omega} \nabla\left(c^{2} \phi\right) \cdot \nabla u \mathrm{~d} x+\int_{\partial \Omega} c^{2} \phi \hat{n} \cdot \nabla u \mathrm{~d} x \] Equipped with the boundary conditions, Eq. (11) is called the weak formulation of Eq. (10). It can be shown that if Eq. (11) holds for all \(\phi \in V\), it has a unique solution \(u \in V\). This solution is called the weak solution. The classical solutions of Eq. (10) are also weak solutions. However, conversely, weak solutions must have sufficient smoothness to be the classical solutions, which dependents both on the shape of the boundary \(\partial \Omega\) and the regularity of \(c^{2} f\).
On the other hand, we can also use the energy conservation property of the wave equation in the numerical analysis: \[ \begin{aligned} & \frac{1}{2} \frac{\partial}{\partial t} \int_{\Omega}\left[\left(\frac{\partial u}{\partial t}\right)^{2}+c^{2}(\nabla u)^{2}\right] \mathrm{d} x \\ =& \int_{\partial \Omega} c^{2}\left(\frac{\partial u}{\partial t}\right)(\hat{n} \cdot \nabla u) \mathrm{d} x-\int_{\Omega}\left(\frac{\partial u}{\partial t}\right)\left[\left(\nabla c^{2}\right) \cdot \nabla u+c^{2} f\right] \mathrm{d} x \end{aligned} \] which was computed by multiply Eq. (10) by \(\frac{\partial u}{\partial t}\) and integrate over the domain \(\Omega\).
Unlike the rest part of waves, the leading wavefront represents the transport of energy. Therefore, it is strictly subject to the constraint of causality. Moreover, the hypersurface of the wavefront (denoted as \(S\) ) is a null hypersurface. Its normal vector \(k^{a}=\nabla^{a} S\) is a null vector \(k^{a} k_{a}=0 .\) And the integral curves of \(k^{a}\) are null geodesics, which satisfy \(k^{a} \nabla_{a} k^{b}=0\) if \(k^{a}\) is presented in terms of an affine parameter. The equations for null geodesics can be presented as: \[ \frac{d^{2} \mu}{d \varphi^{2}}+\mu=-\frac{1}{2} \frac{\partial}{\partial \mu}\left[\mu^{2} \zeta(M, \mu)\right] \]
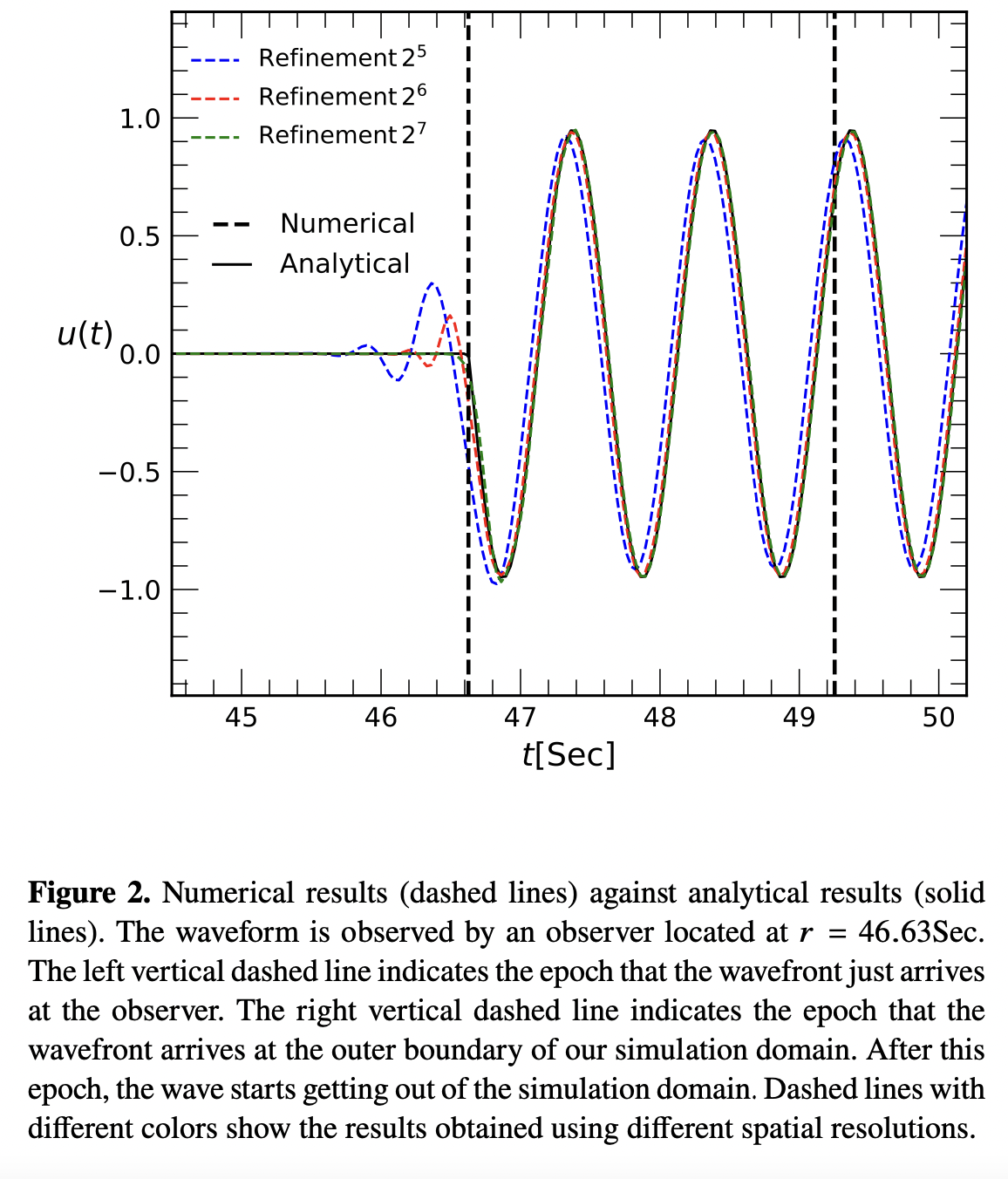
7-23
Do gravitational waves confirm Hawking's area law?
Review the GW190514 testing of BH's no-hair theorem and the BH's area law done mostly by Isi and talk about the philosophy aspect of such tests.
Kerr remnant BH's area: \[ A_{K}=8 \pi\left(\frac{G M_{B H}}{c^{2}}\right)^{2}\left(1+\sqrt{1-a^{2}}\right) \]
Review paper from Department of Philosophy, University of Haifa, Israel.
7-26
Effect of the inner horizon on the black hole thermodynamics: Reissner-Nordström black hole and Kerr black hole
Several approaches to investigate the RN/Kerr BHs' thermodynamics: the entropy and Hawking radiation tempetature are determined by the correlations between the two horizons——they depend only on mass \(M\) and not angular momentum \(J\) and charge \(Q\).
In RN BH cases, using semiclassical quantum tunneling can obtain a different entropy: \[ \tilde{S}_{\mathrm{RN}}=4 \pi M^{2} \] which can also be expressed as: \[ \tilde{S}_{\mathrm{RN}}=\left(\sqrt{S_{+}}+\sqrt{S_{-}}\right)^{2} \] since for RN BHs: \(S_{\mathrm{RN}}\left(r_{+}\right)=\pi r_{+}^{2}=\pi\left(M+\sqrt{M^{2}-Q^{2}}\right)^{2}\).
While considering the Kerr black hole, it was proved that when vary the parameter \(\hbar\) as Minkowski metric in effective theory (adiabatic transformation), the radius form: \[ r_{+} \sim 2 \frac{\hbar M}{E_{P}^{2}}, r_{-} \sim \frac{J^{2} E_{P}^{2}}{2 M^{3} \hbar} \] will make entropy only depends on the outer horizon at \(\hbar\rightarrow\infty\) since the outer horizon grows, the inner horizon shrinks. Thus: \[ S_{\mathrm{Kerr}}(J, M)=S_{\mathrm{Kerr}}(J=0, M)=4 \pi \frac{M^{2}}{E_{P}^{2}} \] And this will be similar in KN BH: \[ S_{\mathrm{KN}}(J, Q, M)=S(J=0, Q=0, M)=4 \pi \frac{M^{2}}{E_{P}^{2}} \]
Possibility of Primordial black holes Collision with Earth and the Consequences
Calculate the chance of primordial black holes heating the interior of the earth (due to two mechanisim: dynamical friction and accretion) is almost zero (\(10^{−11}Gyr^{-1}\)).
A lognormal mass function of PBHs is: \[ \psi\left(M_{i}\right)=\frac{1}{\sqrt{2 \pi} \sigma M_{i}} \exp \left[-\frac{\log ^{2}\left(M_{i} / M_{c}\right)}{2 \sigma^{2}}\right] \] where \(M_c\) is the mass peak.
The deceleration equation of BH due to friction is: \[ \frac{d \mathbf{v}_{b h}}{d t}=-\frac{4 \pi \ln (\Lambda) G^{2} \rho_{e} M_{b h}}{v_{b h}^{3}}\left[\operatorname{erf}(X)-\frac{2 X}{\sqrt{\pi}} e^{-X^{2}}\right] \mathbf{v}_{b h} \] where \(\rho_e\) is the density of earth and \(\ln \Lambda\) is the column logarithm: \[ \ln \Lambda=\ln \frac{b_{\max } \sigma_{e}^{2}}{G\left(M_{b h}+m\right)} \] other details can be seen in the origin article.
Constraining parameters of low mass merging compact binary systems with Einstein Telescope alone
Test the parameter estimation ability of Einstein Telescope working alone. Combine all segment informations of the antenna and investigate the low mass cases with mock data.
A source dependent quantity in L.H.S can be obtained by individually measured characteristic of each segment in R.H.S: \[ \Lambda \equiv\left(\frac{8 r_{0}}{D_{L}}\left(\frac{\mathcal{M}_{z}}{\mathcal{M}_{B N S}}\right)^{5 / 6}\right)^{-1} \approx \frac{\Theta_{e f f}^{i} \sqrt{\zeta^{i}\left(f_{i-1}, f_{i}\right)}}{\rho_{e f f}^{i}} \]
To combine the segment information together, the SNR for \(i_{th}\) segment in \(j_{th}\) detector should also be considered: \[ \rho_{j}^{i} \approx 8 \Theta_{j}^{i} \frac{r_{0}}{D_{L}}\left(\frac{\mathcal{M}_{z}}{\mathcal{M}_{B N S}}\right)^{5 / 6} \sqrt{\zeta^{i}\left(f_{i-1}, f_{i}\right)} \] where \(\zeta^{i}\left(f_{i-1}, f_{i}\right)=\frac{1}{x_{7 / 3}} \int_{f_{i-1}}^{f_{i}} \frac{d f\left(\pi M_{\odot}\right)^{2}}{\left(\pi f M_{\odot}\right)^{7 / 3} S_{h}(f)}\) and \(\Theta_{j}^{i} \equiv 2\left[\left(F_{+}^{i}\right)^{2}\left(1+\cos ^{2} \iota\right)^{2}+4\left(F_{\times}^{i}\right)^{2} \cos ^{2} \iota\right]_{j}^{1 / 2}\).
So that the effective function \(\Theta_{e f f}^{i}\) is given by: \[ \left(\Theta_{e f f}^{i}\right)^{2}=\left(\Theta_{1}^{i}\right)^{2}+\left(\Theta_{2}^{i}\right)^{2}+\left(\Theta_{3}^{i}\right)^{2}. \]
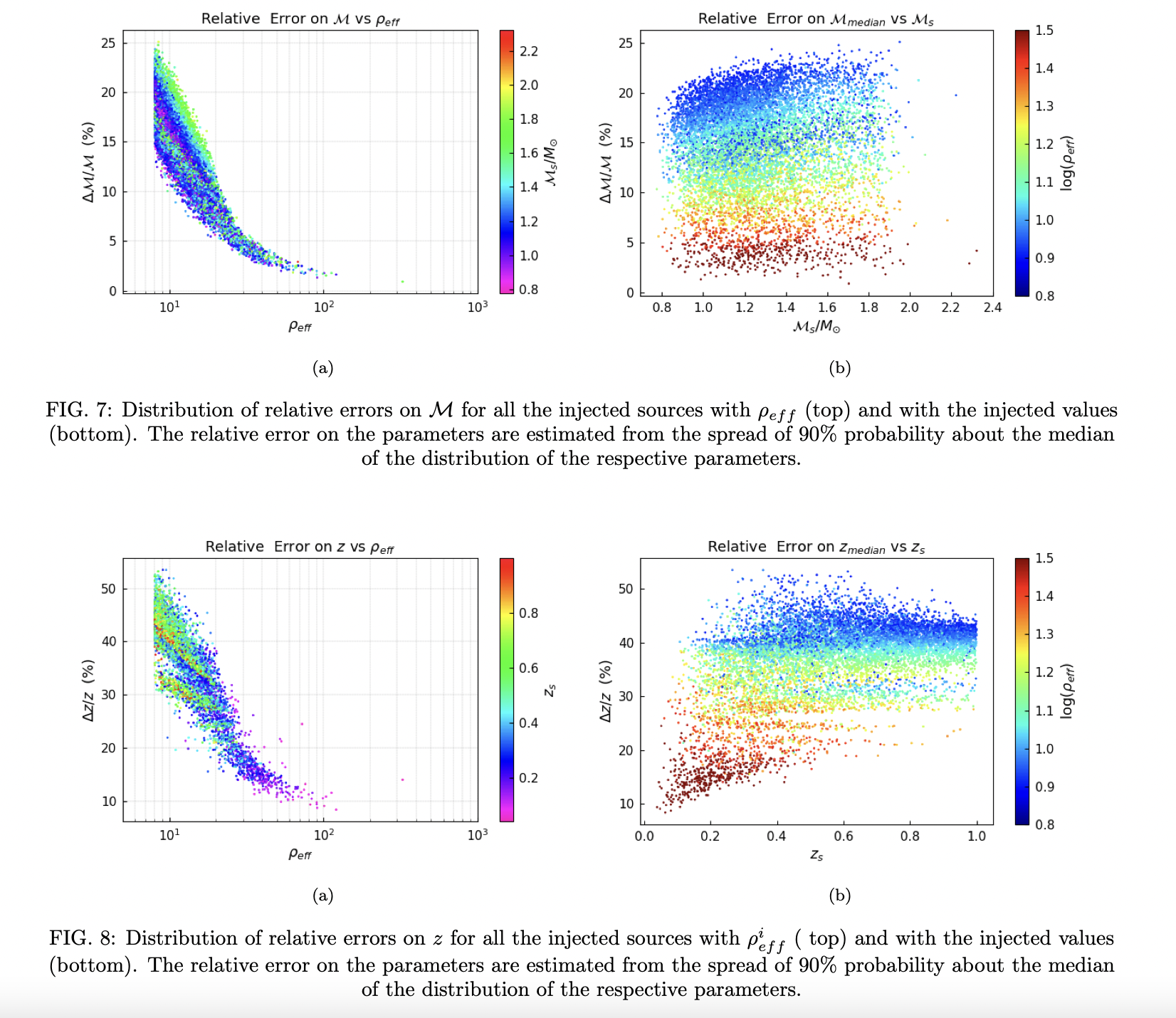
7-27
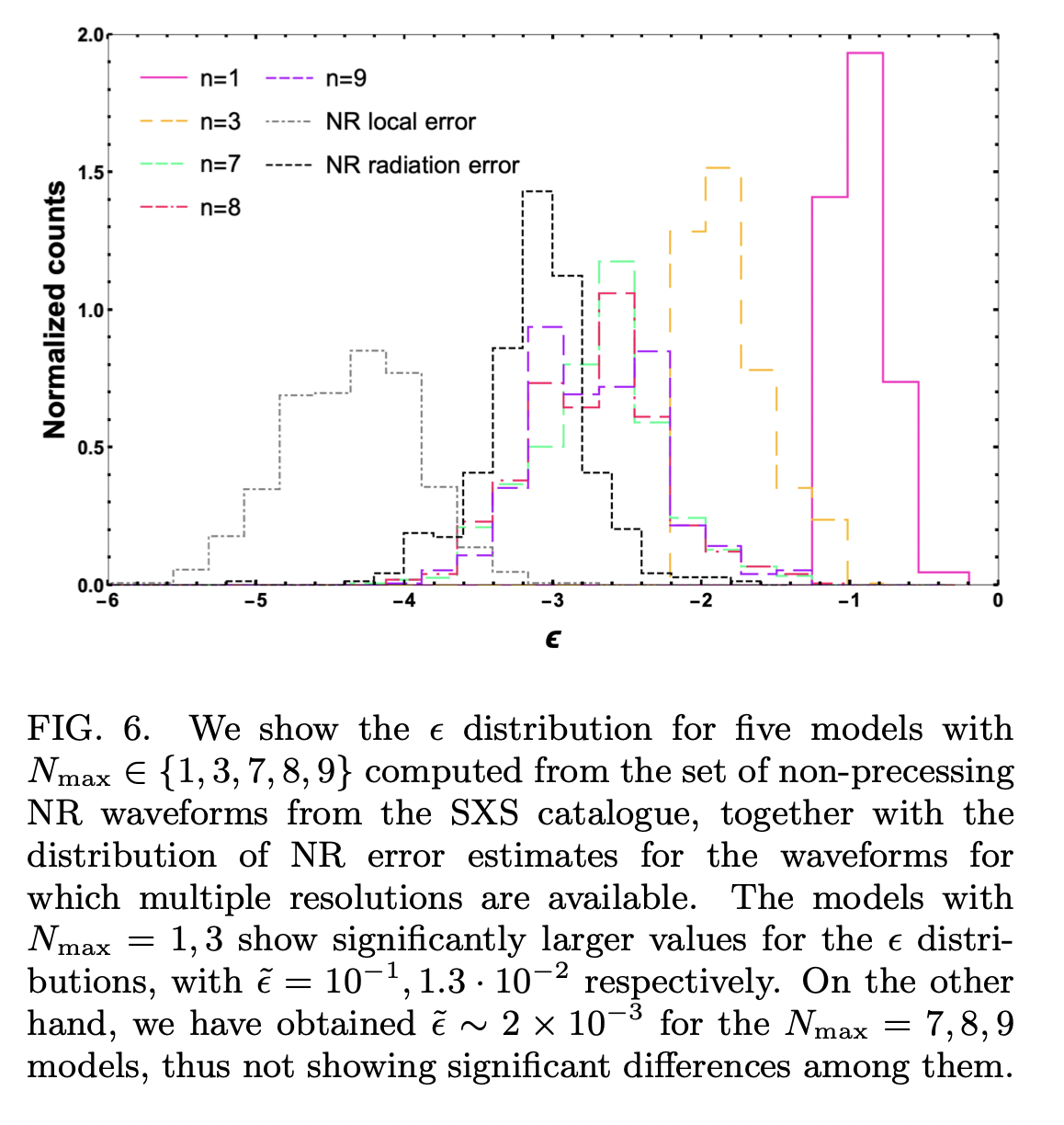
High-overtone fits to numerical relativity ringdowns: beyond the dismissed n=8 special tone
Use 610 NR data from SXS and 2 from RIT catalog to fit high overtone models (\(N_{max}=16\)). Vary mass and spin and see how their obtained values of fitting deviate from the true values. Discuss about the application of including higher overtones in the model.
The final mass and final spin provided by NR catalogues are quasi-local on the apparent horizon (AH). So, the black hole spin \(S\) is obtained from Killing vectors \(\phi^i(k)\) and the extrinsic curvature \(K_{ij}\) at the AH and integrate them over the induced AH area: \[ S_{\phi_{(k)}}=\frac{1}{8 \pi} \int_{\mathrm{AH}} \phi_{(k)}^{i} s^{j} K_{i j} d A \] where \(s^j\) is the outgoing spacelike unit normal vector and \(S_{\phi_{(k)}}\) the spin component along Killing vector. The final mass relies on the spin \(S\) in the Christodoulou formula for uncharged BH: \[ \left(M_{f}^{1}\right)^{2}=M_{\mathrm{irr}}^{2}+\frac{S^{2}}{4 M_{\mathrm{irr}}^{2}} \]
Radiation based mass and spin: \[ \begin{array}{l} M_{f}^{\mathrm{r}}=1-\lim _{r \rightarrow \infty} \frac{r^{2}}{16 \pi} \int_{t^{\prime}} \sum_{l m}\left|\frac{d h_{l m}}{d t}\right|^{2} d t^{\prime} \\ a_{f}^{\mathrm{r}}=J_{\mathrm{in}}+\lim _{r \rightarrow \infty} \frac{r^{2}}{16 \pi} \operatorname{Re}\left[\int_{t^{\prime}} \sum_{l m} m h_{l m}^{*} \frac{d\left(h_{l m}\right)}{d t} d t^{\prime}\right] \end{array} \] where \(h\) is the gravitational wave strain, \(ψ_4 = {d^2h/{dt^2}}\) and \(J_{in}\) the initial ADM dimensionless angular momentum.
A Mission to Nature's Telescope for High-Resolution Imaging of an Exoplanet
- Describes a novel mission design to make spacecraft get to the focal region ( ∼550 AU from the Sun) and obtain high resolution images of exoplanets from the solar gravitational lens (SGL).
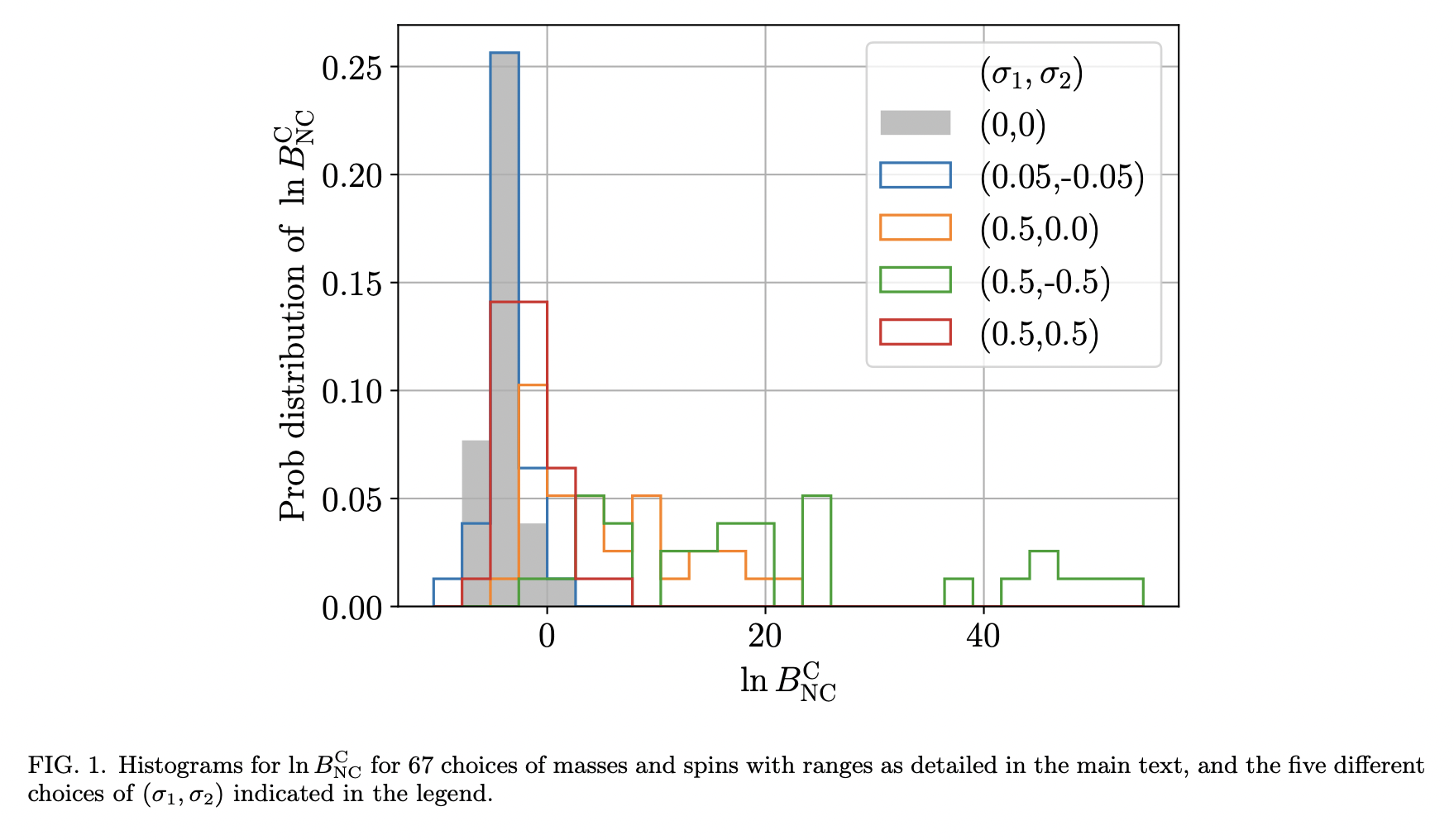
Bounding dark charges on binary black holes using gravitational waves
Using bayesian analysis of GWTC-2 (assume charged) to bound the charge-to-mass ratios of BHs in a hidden U(1) symmetry Einstein-Maxwell theory.
To describe the interaction between the hidden sector and gravity, we introduce Einstein-Maxwell action: \[ S=\int d^{4} x \sqrt{-g}\left[\frac{R}{16 \pi}-\frac{1}{4} F_{\mu \nu} F^{\mu \nu}+4 \pi A_{\mu} j^{\mu}\right] \]
The bayesian factor: \[ B_{\mathrm{NC}}^{\mathrm{C}} \equiv \frac{p\left(d \mid \mathcal{H}_{\mathrm{C}}, \mathcal{I}\right)}{p\left(d \mid \mathcal{H}_{\mathrm{NC}}, \mathcal{I}\right)} \] will be applied in the analysis of simulation——inspiral waveform assuming charged with \(\sigma_{1} \equiv q_{1} / m_{1}, \sigma_{2} \equiv q_{2} / m_{2}\).
7-28
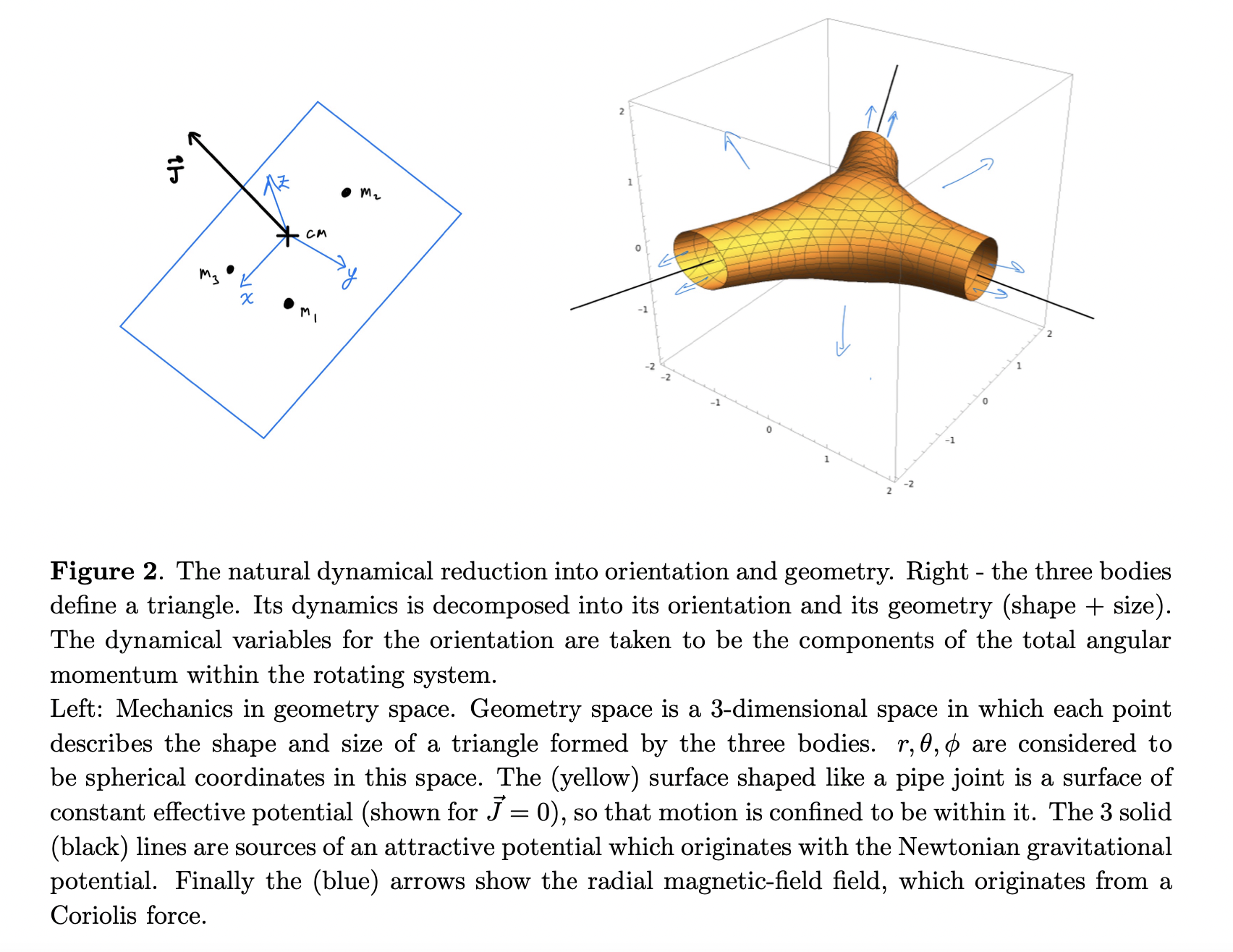
Natural dynamical reduction of the three-body problem
Reduction of three-body problem as a configuration defines one triangle, and its orientation in space. Generalization of the Euler-Lagrange equations to non-coordinate velocities make this a novel idea to introduce the orientation variables in 3d curved space.
In order to not break the symmetry between bodies, it was suggested by Lagrange’s solution to the cubic equation that we should focus on the roots of the polynomial equation, hence we define: \[ \vec{w}:=\vec{r}_{1}+\eta \vec{r}_{2}+\bar{\eta} \vec{r}_{3} \] when given \(\vec{w}\), the relative positions can be expressed by: \[ \vec{r}_{23}=\frac{1}{j \sqrt{3}}(\vec{w}-\vec{\bar{w}}) \] replacing \(w \rightarrow \eta w\) in this expression gives \(\vec{r}_{12}\), and \(w \rightarrow \bar{\eta} w\) gives \(\vec{r}_{31}\).
While for the four-body problem: \[ \begin{array}{l} \vec{s}_{1}=\vec{r}_{1}-\vec{r}_{2}-\vec{r}_{3}+\vec{r}_{4} \\ \vec{s}_{2}=-\vec{r}_{1}+\vec{r}_{2}-\vec{r}_{3}+\vec{r}_{4} \\ \vec{s}_{3}=-\vec{r}_{1}-\vec{r}_{2}+\vec{r}_{3}+\vec{r}_{4} \end{array} \] so they contain 9 degrees of freedom to be decomposed.
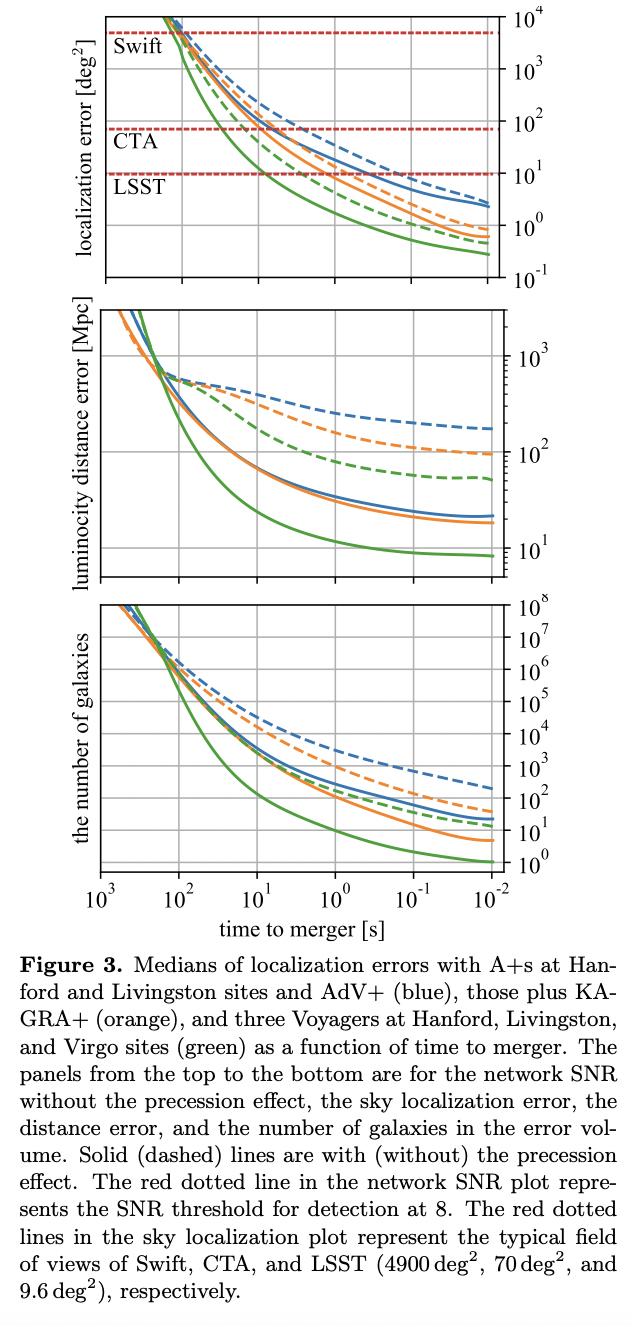
Early warning of precessing neutron-star black-hole binary mergers with the near-future gravitational-wave detectors
The early warning before merger (if detectting when and where the events happen) can act as an alert for merger signal afterhand with EM telescopes pointed to the sources. Considering precessing neutron-star black-hole (NSBH) binaries coalescence events, this work predicted that it can be localized in 100 deg2 on the sky before ∼ \(10^{–40} s\) of time to merger once per year with 2.5G detectors, like KAGRA+.
The event rate of GW as a function of redshift \(z\) is given by (Cutler et al. 2008): \[ \frac{\mathrm{d} N}{\mathrm{~d} z}=\frac{4 \pi r(z)^{2} \dot{n}(z) T_{\mathrm{obs}}}{(1+z) H(z)} \] where \(T_{\mathrm{obs}}\) is the observation time, \(\dot{n}(z)\) is the merger rate per unit comoving volume and unit proper time at redshift \(z\), \(r(z)\) is the comoving distance and \(H(z)\) is the Hubble parameter.
Gravitational Radiation from Accelerating Jets
Relativistic jets like those exist within some core collapse SNe have prospects to be detected by sub-Hz detectors.
The time of arrival from different angle of the jet is given by: \[ \tilde{t}_{\mathrm{o}}\left(\theta_{\mathrm{v}}\right)=\left(1-\beta \cos \Delta \theta_{\mathrm{v}}\right) t_{\mathrm{acc}} \]
It was suggested by (Kobayashi et al. 1997) that the \(\dot{m}(t)\) is related to GRB light curve, the paper used spectra for long and short GRBs observed by the Burst and Transient Source Experiment (BATSE) here.
For long GRBs: \[ \tilde{h}_{l}(f)=C_{l}(f) \tilde{h}(f) \propto\left\{\begin{array}{ll} f^{-1}, & f<f_{l} \\ f^{-1.75}, & f_{l}<f<\tilde{f}_{\mathrm{o}} \\ f^{-0.75-\alpha}, & \tilde{f}_{\mathrm{o}}<f \end{array}\right. \] For short GRBs: \[ \tilde{h}_{s}(f)=C_{s}(f) \tilde{h}(f) \propto\left\{\begin{array}{ll} f^{-1}, & f<f_{s} \\ f^{-1.92}, & f_{s}<f<\tilde{f}_{\mathrm{o}} \\ f^{-0.92-\alpha}, & \tilde{f}_{\mathrm{o}}<f \end{array}\right. \]
7-29
Multipole decomposition of gravitational lensing
Using an infinite set of symmetric trace free (STF) tensor multipole mass moments to investigate the optical properties of a generic gravitational lens (not limited to spherically symmetric gravitational fields). Which can be applied to realistic astrophysical systems and solar gravitational lens (SGL).
When considered the case of a lens body with arbitrary composition, the potential of the gravitational field can be expanded in terms of spherical harmonics: \[ U(\mathbf{r})=\frac{G M}{r}\left(1+\sum_{\ell=2}^{\infty} \sum_{k=0}^{+\ell}\left(\frac{R}{r}\right)^{\ell} P_{\ell k}(\cos \theta)\left(C_{\ell k} \cos k \phi+S_{\ell k} \sin k \phi\right)\right)+\mathcal{O}\left(c^{-4}\right) \] in terms of STF tensors, the above scalar may equivalently be given in the following form: \[ U(\mathbf{r})=G \int \frac{\rho\left(\mathbf{r}^{\prime}\right) d^{3} \mathbf{r}^{\prime}}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|}=G M \sum_{\ell=0}^{\infty} \frac{(-1)^{\ell}}{\ell !} \mathcal{T}^{\left.<a_{1} \ldots a_{\ell}\right.>} \frac{\partial^{\ell}}{\partial x^{\left.<a_{1} \ldots \partial x^{a_{\ell}}\right.>}}\left(\frac{1}{r}\right)+\mathcal{O}\left(c^{-4}\right) \] where \(M\) is the post-Newtonian mass of the body, and \(\mathcal{T}^{\left.<a_{1} \ldots a_{\ell}\right.>}\) are the normalized STF multipole moments defined as: \[ M=\int d^{3} \mathbf{r}^{\prime} \rho\left(\mathbf{r}^{\prime}\right), \quad \mathcal{T}^{\left.<a_{1} \ldots a_{\ell}\right.>}=\frac{1}{M} \int d^{3} \mathbf{r}^{\prime} \rho\left(\mathbf{r}^{\prime}\right) x^{\prime<a_{1} \ldots a_{\ell}>} \] After simple derivation, the gravitational phase shift takes the most general form: \[ \begin{array}{r} \varphi(\mathbf{b})=k r_{g} \sum_{\ell=0}^{\infty} \frac{(-1)^{\ell}}{\ell !} \mathcal{T}^{<a_{1} \ldots a_{\ell}>}\left\{\partial_{\left\langle a_{1}\right.} \ldots \partial_{a_{\ell}>}\left\{\ln \left(\frac{\sqrt{b^{2}+\tau^{2}}+\tau}{b}\right)+\ln \left(\frac{\sqrt{b^{2}+\tau_{0}^{2}}+\left|\tau_{0}\right|}{b}\right)\right\}+\right. \\ \left.+\sum_{p=1}^{\ell} \frac{\ell !}{p !(\ell-p) !} k_{<a_{1}} \ldots k_{a_{p}} \partial_{a_{p+1}} \ldots \partial_{a_{\ell}>}\left\{\frac{\partial^{p-1}}{\partial \tau^{p-1}} \frac{1}{\sqrt{b^{2}+\tau^{2}}}+\frac{\partial^{p-1}}{\partial \tau_{0}^{p-1}} \frac{1}{\sqrt{b^{2}+\tau_{0}^{2}}}\right\}\right\} \end{array} \] and also the eikonal phase shift: \[ \xi_{b}(\mathbf{b})=-k r_{g} \sum_{\ell=2}^{\infty} \frac{(-1)^{\ell}}{\ell !} \mathcal{T}^{<a_{1} \ldots a_{\ell}>} \partial_{<a_{1}} \ldots \partial_{a_{\ell}>} \ln k b+\mathcal{O}\left(r_{g}^{2}\right) \] can be generalized as well.
The light deflection angle can be computed as: \[ \boldsymbol{\theta}_{g}=\frac{2 r_{g}}{b}\left\{\mathbf{e}_{b}+\sum_{\ell=2}^{\infty} \frac{(2 \ell-2) ! !}{(\ell-1) ! b^{\ell}} \sqrt{t_{\ell}^{+2}+t_{\ell}^{\times 2}}\left(\mathbf{e}_{b} \cos \left[\ell\left(\phi_{\xi}-\phi_{\ell}\right)\right]+\mathbf{e}_{\phi_{\xi}} \sin \left[\ell\left(\phi_{\xi}-\phi_{\ell}\right)\right]\right)\right\}. \]
Normal Approximate Likelihoods to Gravitational Wave Events
Using only 3 key dimensions: \(\left(\mathcal{M}_{c}, \eta, \chi_{\mathrm{eff}}\right)\) to approximate the posterior distributions of a Gaussian likelihood, and testing this technique with GWTC-1 and GWTC-2. The highly accurate results also indicate the potential usage of these approximation to generate GW events efficiently, which have wide application to investigate GW population astrophysics.
The definition of the three parameters are as followed: \[ \eta=\frac{m_{1} m_{2}}{\left(m_{1}+m_{2}\right)^{2}},\quad \mathcal{M}_{c}=\eta^{3 / 5} M^{2 / 5},\quad \chi_{\mathrm{eff}}=\left(\boldsymbol{\chi}_{1} m_{1}+\chi_{2} m_{2}\right) \cdot \hat{\mathbf{L}} / M. \] for clarity, the 3-vector \(\hat{\mathbf{L}}\) is orthogonal to the plane (in Cartesian coordinate system).
The work is theroretically related to several former work like: GWBENCH, RIFT, which deeply based on the well-studied Fisher matrix approximation.
To assess the reliability of the Gausssian approximations, this work introduces the KL divergence: \[ \bar{D}_{K L}=\sqrt{\sum_{k} D_{K L}\left(p_{k} \| q_{k}\right)^{2}} \] where \(p_{k}\) represent the one-dimensional Gaussian distributions and \(q_k\) represent the KDE-based estimate for the likelihood (where the idea is to minimize \(\sum_{k}\left|\hat{q}\left(x_{k}\right)-G\left(x_{k}-\mu, \Sigma\right)\right|^{2}\)).
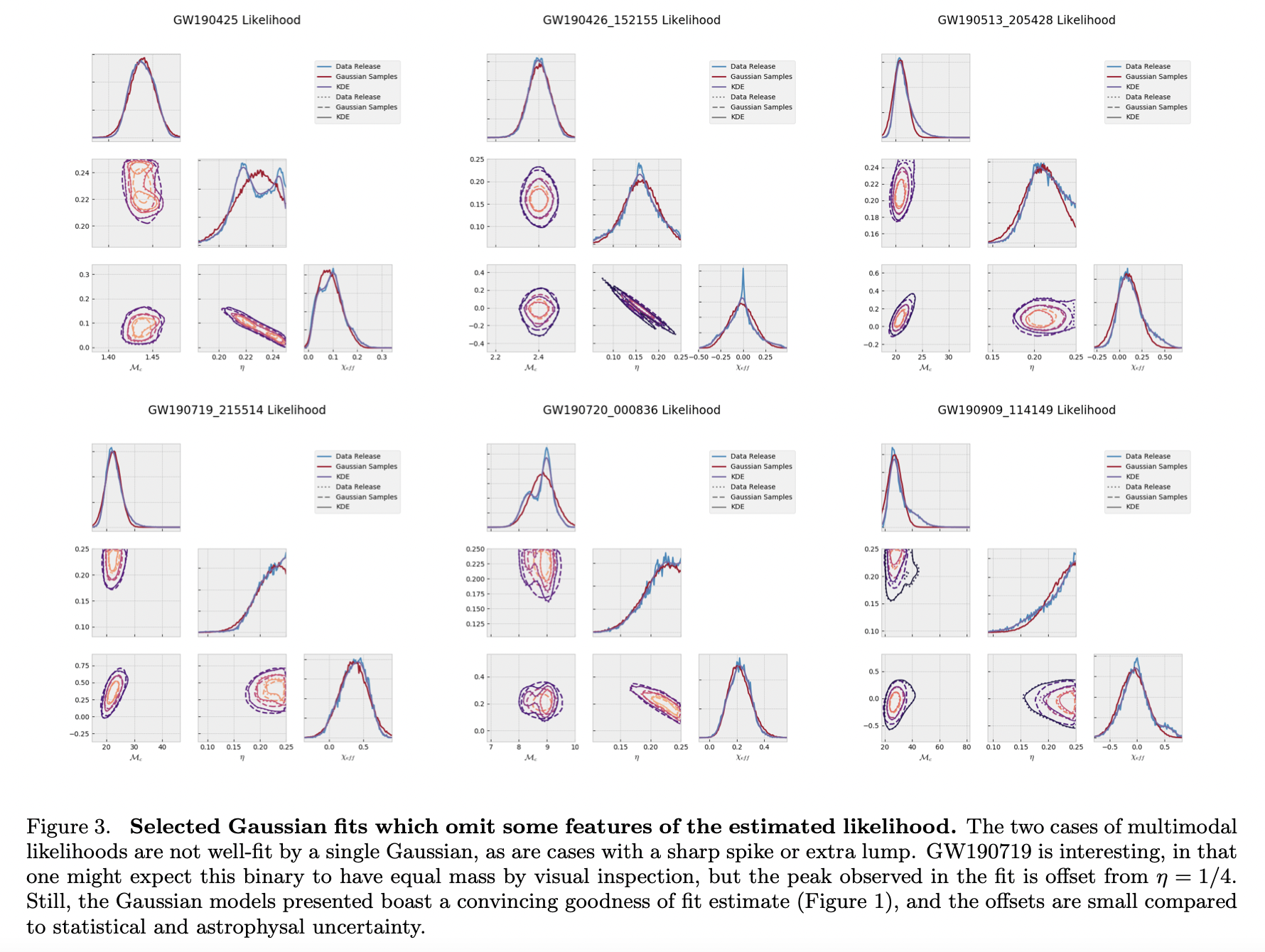
7-30
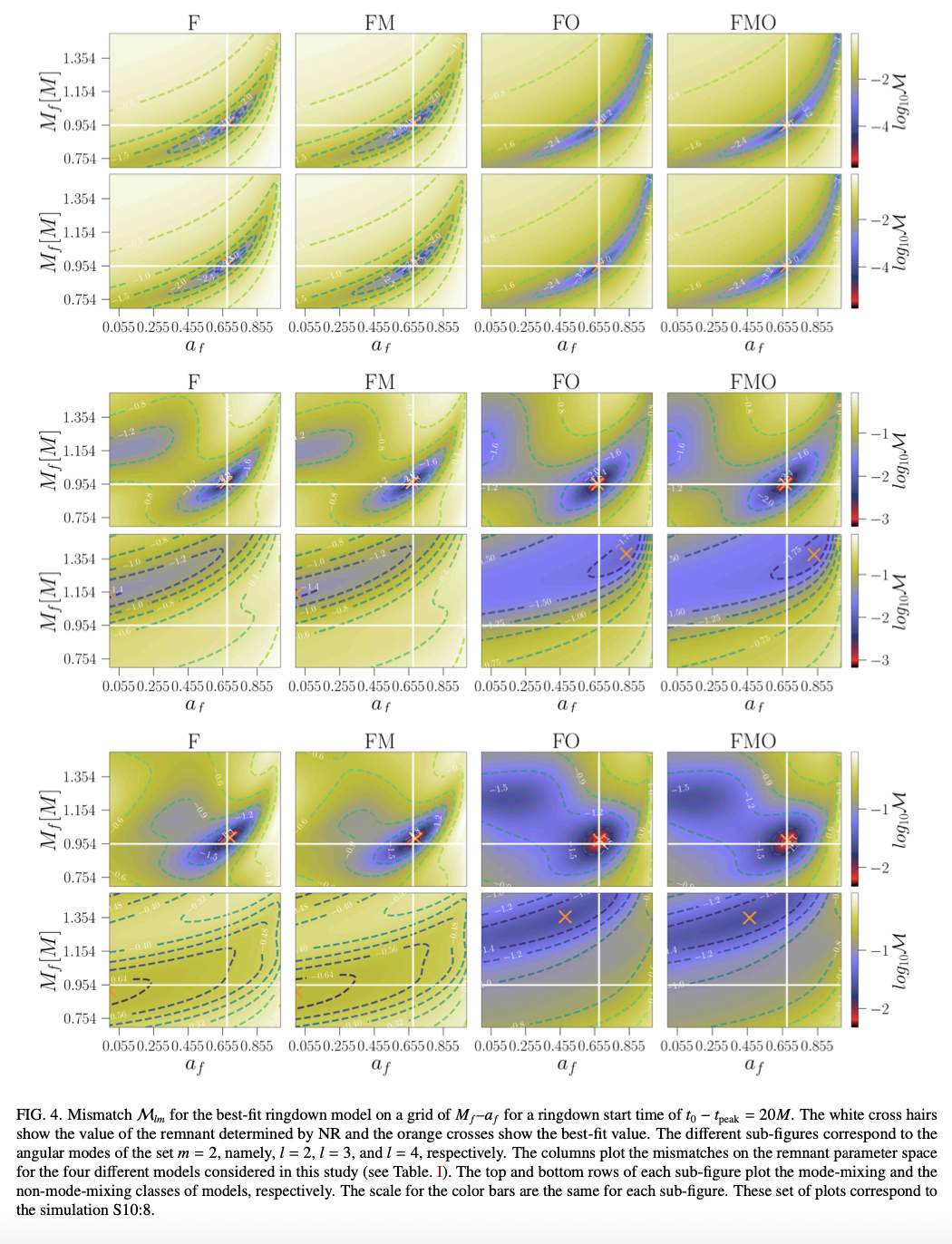
Overtones, mirror modes, and mode-mixing in binary black hole mergers
Test the potential contribution of first overtone/mirror modes/mode mixing effects with the fitting of numerical relativity post-merger GW data and the recovery of mass and spin from a grid method.
The effect of mode-mixing in a given spherical harmonic mode is determined by two independent factors:
the relative excitation amplitudes of the QNMs with the same \(m\) and
the magnitude of the mixing-coefficients between them.

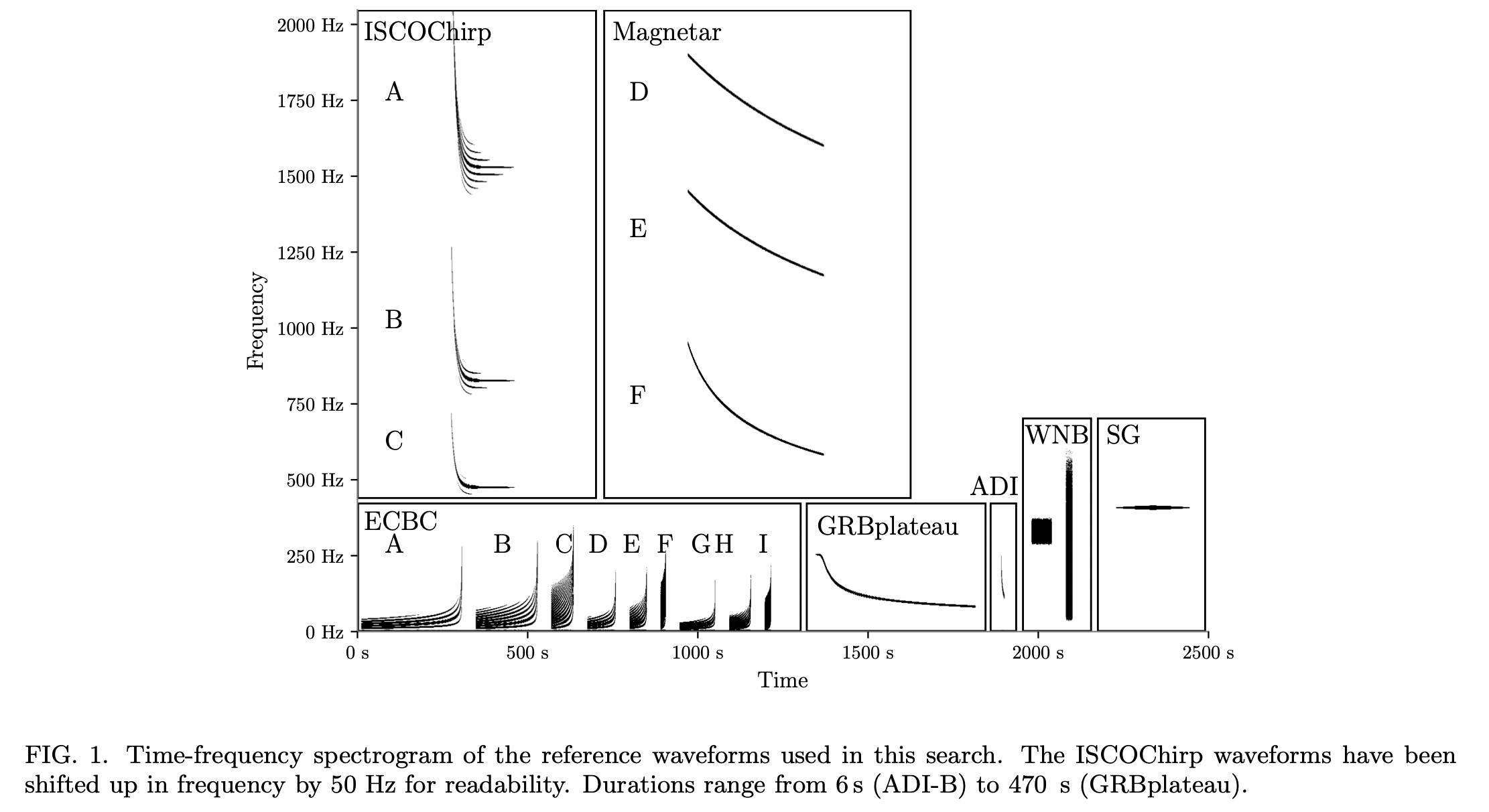
All-sky search for long-duration gravitational-wave bursts in the third Advanced LIGO and Advanced Virgo run
- Not well-defined search for “long” \(\gtrsim 1 \mathrm{~s}\) transient gravitational wave signals. Found no significant triggers within this parameter space ( \(2 – 500 \mathrm{~s}\) in duration and a frequency band of \(24 − 2048\) Hz).
- The potential astrophysical models could be:
- Post-merger magnetars (Magnetar).
- Black hole accretion disk instabilities (ADI).
- Newly formed magnetar powering a gamma-ray burst plateau (GRBplateau).
- Eccentric inspiral-merger-ringdown compact binary coalescence waveforms (ECBC).
- Broadband chirps from innermost stable circular orbit waves around rotating black holes (ISCOchirp).
August
8-5
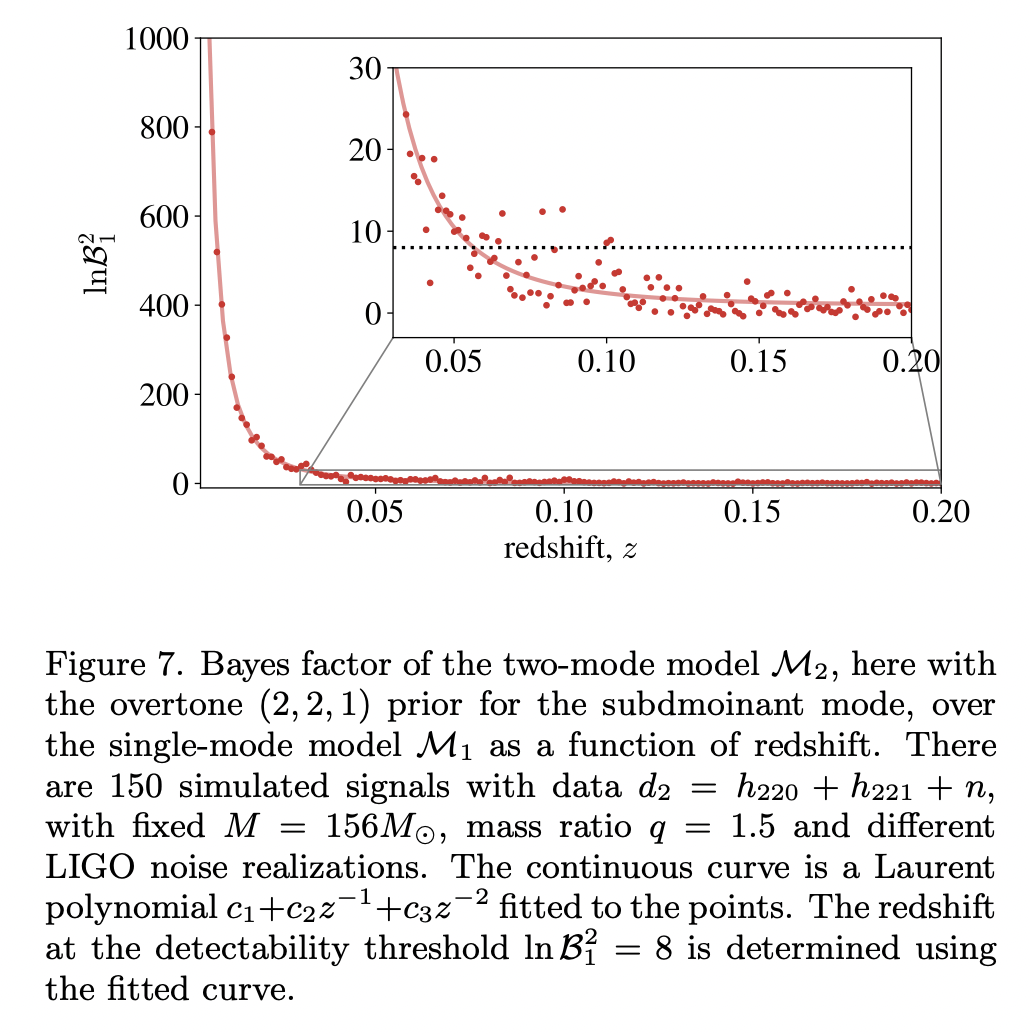
Black hole spectroscopy horizons for current and future gravitational wave detectors
Improving the detectability of seconday modes with a Bayes factor threshold \(\ln B_1^2 > 8\) instead of the standard Rayleigh criterion supplied with a Fisher matrix error estimation that commly used before. Predict the event rate of such detectable merger events with the distance (averaged in sky location and binary inclination) of horizons.
Coherent mode stacking has been proposed to use multiple measurements to increase the SNR of the subdominant quasinormal modes. But the original proposal is not easy to be applied to overtones.
The "Rayleigh criterion" used here is: \[ \begin{aligned} &\Delta f_{\ell m n, \ell^{\prime} m^{\prime} n^{\prime}}>\max \left(\sigma_{f_{\ell m n}}, \sigma_{f_{\ell^{\prime} m^{\prime} n^{\prime}}}\right) \\ &\Delta \tau_{\ell m n, \ell^{\prime} m^{\prime} n^{\prime}}>\max \left(\sigma_{\tau_{\ell m n}}, \sigma_{\tau_{\ell^{\prime} m^{\prime} n^{\prime}}}\right) \end{aligned} \] where also uses the definitions: \[ \begin{aligned} &\Delta f_{\ell m n, \ell^{\prime} m^{\prime} n^{\prime}} \equiv\left|f_{\ell m n}-f_{\ell^{\prime} m^{\prime} n^{\prime}}\right| \\ &\Delta \tau_{\ell m n, \ell^{\prime} m^{\prime} n^{\prime}} \equiv\left|\tau_{\ell m n}-\tau_{\ell^{\prime} m^{\prime} n^{\prime}}\right| \end{aligned} \] The errors \(\sigma_{f_{\ell m n}}\) and \(\sigma_{\tau_{\ell m n}}\) needed for the above Rayleigh conditions can be estimated in the Fisher matrix formalism: \[ \Gamma_{a b} \equiv\left\langle\frac{\partial h}{\partial \vartheta^{a}} \mid \frac{\partial h}{\partial \vartheta^{b}}\right\rangle \] where the errors are equal to: \[ \sigma_{\vartheta^{a}}=\sqrt{\left(\Gamma^{-1}\right)^{a a}} \] The probability density distribution for each parameter \(\vartheta^{a}\) (\(\left\{f_{\ell m n}, \tau_{\ell m n}, A_{\ell m n}, \phi_{\ell m n}, f_{\ell^{\prime} m^{\prime} n^{\prime}}, \tau_{\ell^{\prime} m^{\prime} n^{\prime}}, R, \phi_{\ell^{\prime} m^{\prime} n^{\prime}}\right\}\)) is proportional to the multidimensional Gaussian \(\exp \left[-(1 / 2) \Gamma_{a b} \vartheta^{a} \vartheta^{b}\right]\).
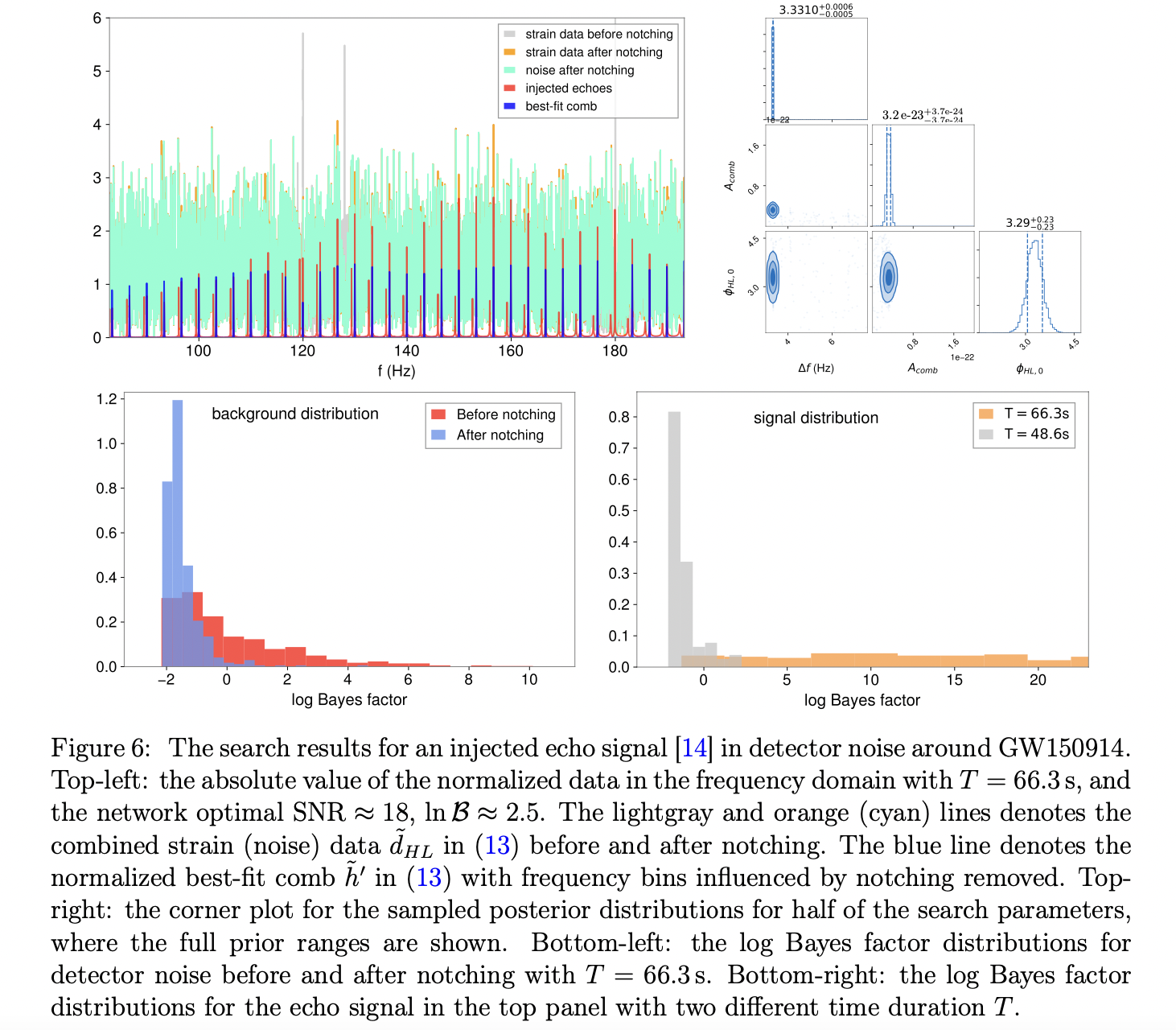
Gravitational wave echoes search with combs
Combs has been proposed to look for the resonance structure of GW echo signals. This paper develops a phase-marginalized likelihood Bayesian algorithm and searches for the resonance structure based on GW150914 and GW151012.
After marginalizing over the signal model phase, and transform the power spectrum density (PSD) into a compact form, we get: \[ \rho_{\mathrm{opt}}^{2}=\sum_{j=1}^{N}\left|\tilde{h}_{j}^{\prime}\right|^{2}, \quad \rho_{\mathrm{mf}}=\frac{1}{\rho_{\mathrm{opt}}} \sum_{j=1}^{N} \ln I_{0}\left(\left|\tilde{d}_{H L, j} \| \tilde{h}_{j}^{\prime}\right|\right) \] while the normalized log-likelihood is: \[ \ln \tilde{\mathcal{L}}(\mathbf{d} \mid \theta)=\rho_{\mathrm{mf}} \rho_{\mathrm{opt}}-\frac{1}{2} \rho_{\mathrm{opt}}^{2} \] in above equations, \(\rho_{\text {opt }}\) denotes the conventional optimal signal-to-noise ratio (SNR), while \(\rho_{\mathrm{mf}}\) quantifies the overlap between the signal and data with no phase information.
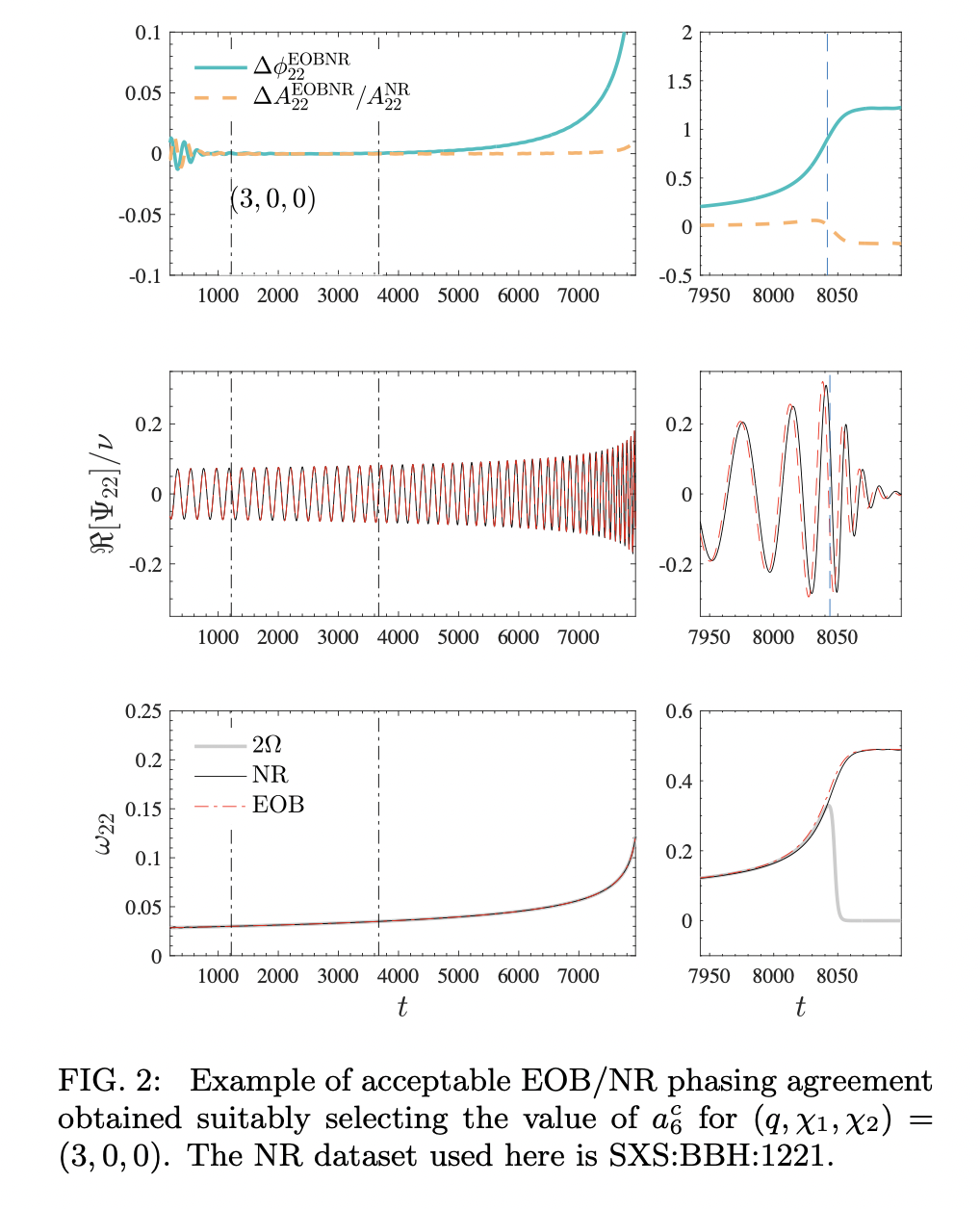
The next generation: Impact of high-order analytical information on effective one body waveform models for noncircularized, spin-aligned black hole binaries
Provideing an improved TEOBResumS waveform model (effective-one-body (EOB) model for spin-aligned BBCs) by adding recently computed high-order PN information in both the orbital and spin sector, and test the EOB/NR agreement with several cases.
The Taylor expansions of the \((A, D)\) potential up to 5PN accuracy read: \[ \begin{aligned} A_{5 \mathrm{PN}}(u)=& 1-2 u+2 \nu u^{3}+\nu\left(\frac{94}{3}-\frac{41 \pi^{2}}{32}\right) u^{4}+\\ &+\left[\left(\frac{2275 \pi^{2}}{512}-\frac{4237}{60}+\frac{128}{5} \gamma_{\mathrm{E}}+\frac{256}{5} \ln (2)\right) \nu+\left(\frac{41 \pi^{2}}{32}-\frac{221}{6}\right) \nu^{2}+\frac{64}{5} \nu \ln (u)\right] u^{5}+\\ &+\nu\left[a_{6}^{c}+\left(-\frac{7004}{105}-\frac{144}{5} \nu\right) \ln (u)\right] u^{6}, \\ D_{5 \mathrm{PN}}(u)=& 1-6 \nu u^{2}-\left(52 \nu-6 \nu^{2}\right) u^{3}+\\ &+\left[\left(\frac{533}{45}+\frac{23761 \pi^{2}}{1536}-\frac{1184}{15} \gamma_{\mathrm{E}}+\frac{6496}{15} \ln (2)-\frac{2916}{5} \ln (3)\right) \nu+\left(-\frac{123 \pi^{2}}{16}+296\right) \nu^{2}-\frac{592}{15} \nu \ln (u)\right] u^{4}+\\ &{\left[\left(-\frac{294464}{175}+\frac{63707 \pi^{2}}{512}+\frac{2840}{7} \gamma_{\mathrm{E}}-\frac{120648}{35} \ln (2)+\frac{19683}{7} \ln (3)\right) \nu+\right.} \\ &\quad+\left(-d_{5}^{\nu^{2}}-\frac{2216}{105}+\frac{6784}{15} \gamma_{\mathrm{E}}+\frac{326656}{21} \ln (2)-\frac{58320}{7} \ln (3)\right) \nu^{2}+ \\ &\left.\quad+\left(-\frac{1285}{3}+\frac{205 \pi^{2}}{16}\right) \nu^{3}+\left(\frac{1420}{7} \nu+\frac{3392}{15} \nu^{2}\right) \ln (u)\right] u^{5} \end{aligned} \] where \(A\) and \(B\) are the EOB potentials (with spin-spin interactions included) and \(D = AB\) (for non-spinning systems).
8-6
Stability of the protoneutron stars toward black hole formation
Examine the protoneutron stars (PNS) stability and GWs frequencies from the massive PNS produced by failed supernovae. By solving the radial oscillation equations and adopting the numerical results, it has been found that the PNSs are stable in their evolution against the radial perturbations, while finally becomes unstable before the apparent horizon appears inside the PNS.
The GW signals appearing in the numerical simulations can be classified as:
- Fundamental (f-mode) oscillations of PNS.
- g-mode like oscillations on the region inside the shock radius.
- Standing accretion-shock instability.
The radial perturbation equations of PNS are: \[ \begin{aligned} &\frac{d \xi}{d r}=-\left[\frac{3}{r}+\frac{p^{\prime}}{p+\varepsilon}\right] \xi-\frac{\eta}{r \Gamma} \\ &\frac{d \eta}{d r}=\left[r(p+\varepsilon) e^{2 \Lambda}\left(\frac{\omega^{2}}{p} e^{-2 \Phi}-8 \pi\right)-\frac{4 p^{\prime}}{p}+\frac{r\left(p^{\prime}\right)^{2}}{p(p+\varepsilon)}\right] \xi-\left[\frac{\varepsilon p^{\prime}}{p(p+\varepsilon)}+4 \pi r(p+\varepsilon) e^{2 \Lambda}\right] \eta, \end{aligned} \] where \(p, \varepsilon\), denote the pressure and energy density for the background PNS models, while \(\xi\) and \(\eta\) are perturbative variables given by \(\xi \equiv \Delta r / r\) and \(\eta \equiv \Delta p / p\). And \(\Delta r\), the Lagrangian perturbation of radius. The prime in the equations denotes the radial derivative and the adiabatic index is given by: \[ \Gamma \equiv\left(\frac{\partial \ln p}{\partial \ln n_{\mathrm{b}}}\right)_{s}=\frac{p+\varepsilon}{p} c_{s}^{2} \] where \(n_{\mathrm{b}}, s\), and \(c_{s}\) denote the baryon number density, entropy per baryon, and sound velocity, respectively.
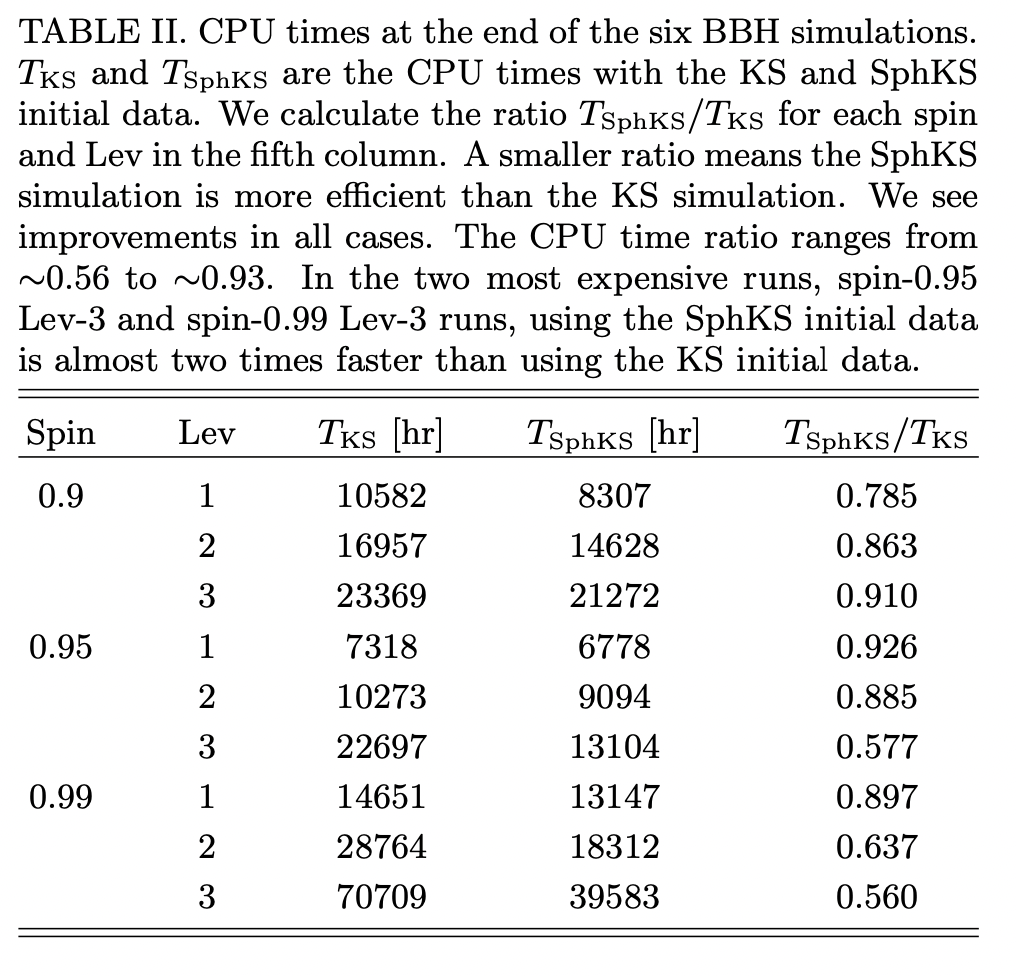
Efficient simulations of high-spin black holes with a new gauge
Developing new gauge conditions (Kerr-Schild-like gauge) for BHs to reduce the computational cost of high-spin BBH simulations. Observing an factor of two reduction in CPU time for the spin-0.99 Lev3 case of SXS.
The spherical KS coordinates are denoted by \(\{t, \bar{x}, \bar{y}, \bar{z}\}\). These are related to the KS coordinates \(\{t, x, y, z\}\) by: \[ \begin{aligned} \frac{\bar{x}}{r} &=\frac{x}{\sqrt{r^{2}+a^{2}}} \\ \frac{\bar{y}}{r} &=\frac{y}{\sqrt{r^{2}+a^{2}}} \\ \bar{z} &=z \end{aligned} \]
8-9
New limits on the Lorentz/CPT symmetry through fifty gravitational-wave events
- Using the 50 GW events from GWTC-1/2, this work constraints the gravitational Lorentz invariance violation's (gLIV) parameter space (34 coefficients) globally by factors ranging from 2 to 7.
- A general gLIV includes anisotropy, dispersion, and birefringence. Previous work mostly emphasized the isotropic birefringent phenomenon, while in this work, the focus was on the anisotropic birefringence of GWs.
Unstable modes of hypermassive compact stars driven by viscosity and gravitational radiation
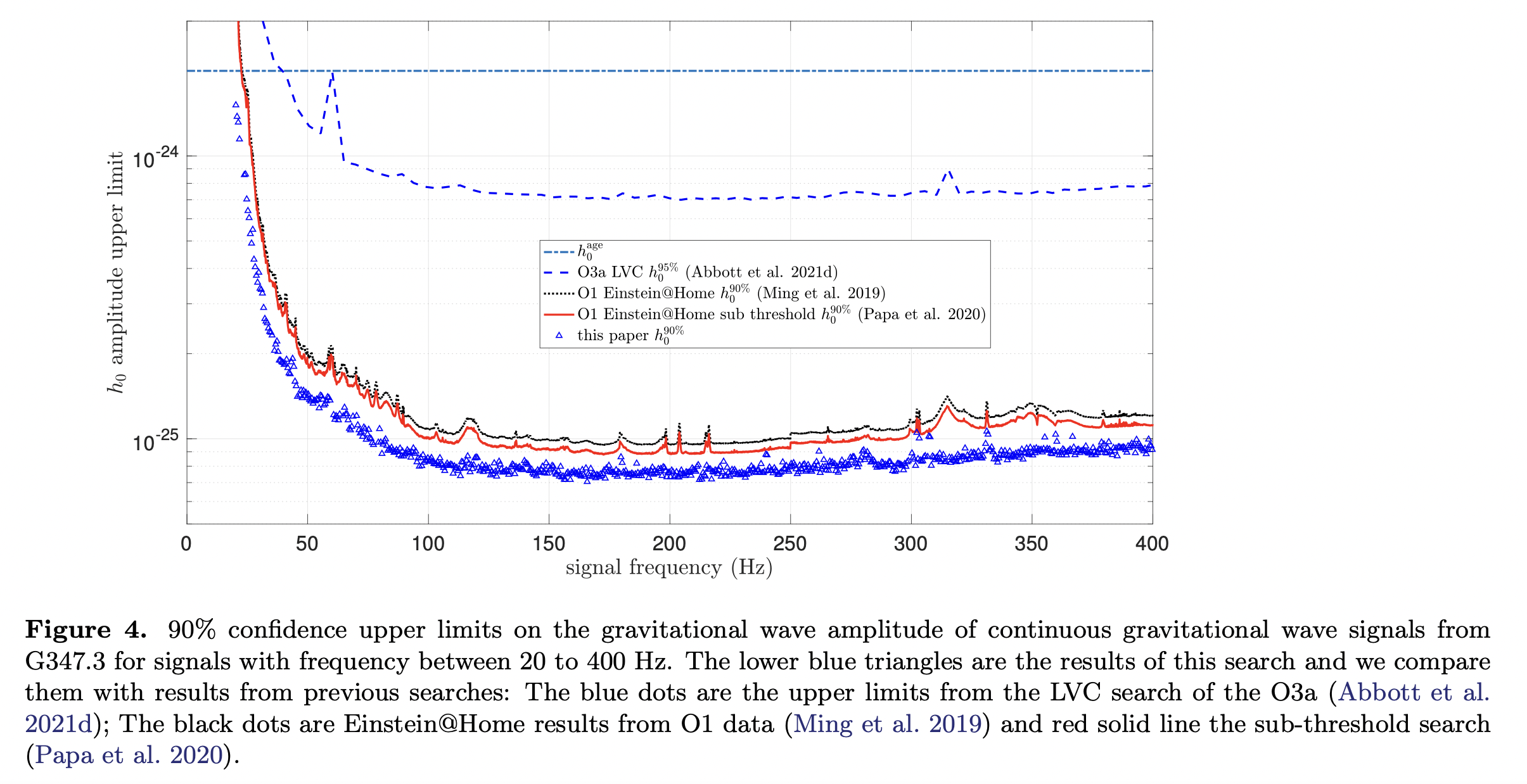
Results from an Einstein@Home search for continuous gravitational waves from G347.3 at low frequencies in LIGO O2 data
Presenting results of a search for periodic gravitational wave signals with frequency between 20 and 400 Hz, from the neutron star in the supernova remnant G347.3-0.5, using LIGO O2 public data. Place the upper limits a factor of 20 smaller than the indirect age-based upper limit of GW intrinsic amplitude.
Useing a “stack-slide” type of search based on the GCT (Global correlation transform) method. Allen 2009; Pletsch 2008, 2010). The data is partitioned in \(N_{\text {seg }}\) segments and each segment spans a duration \(T_{\text {coh }}\). The data of both detectors from each segment \(i\) is searched with a maximum likelihood coherent method to construct the detection statistic, \(\mathcal{F}\)-statistic. The statistics \(\mathcal{F}_{i}\) from the coherent searches of the different segments are summed, and the value of the core detection statistic \(\overline{\mathcal{F}}\) is obtained: \[ \overline{\mathcal{F}}:=\frac{1}{N_{\mathrm{seg}}} \sum_{i=1}^{N_{\mathrm{seg}}} \mathcal{F}_{i} \] In Gaussian noise \(N_{\mathrm{seg}} \times 2 \overline{\mathcal{F}}\) follows a chi-squared distribution with \(4 N_{\mathrm{seg}}\) degrees of freedom, and a noncentrality parameter \(\rho^{2} .\) If a signal is present, \(\rho^{2}\) is proportional to \(\frac{h_{0}^{2} T_{\text {obs }}}{S_{h}}\), where \(S_{h}\) is the strain power spectral density of the noise at the frequency of the signal, and \(h_{0}\) is the signal intrinsic amplitude at Earth.
Gravitational-wave glitches: resonant islands and frequency jumps in non-integrable extreme-mass-ratio inspirals
8-10
Geometric horizons in binary black hole mergers
Measuring the dark matter environments of black hole binaries with gravitational waves
Modified gravitational wave propagation and the binary neutron star mass function
The paper shows that, the narrowness of the mass distribution of binary neutron stars in the current and future observations provide a clear signature of modified gravity by the difference between the reconstruction of the redshift of coalescing binaries from the luminosity distance measured by different modified GW propagation properties.
The deviation is encoded in the propagation equation of gravitational waves (GWs) across cosmological distances which, in modified gravity theories, can take the form: \[ \tilde{h}_{A}^{\prime \prime}+2 \mathcal{H}[1-\delta(\eta)] \tilde{h}_{A}^{\prime}+c^{2} k^{2} \tilde{h}_{A}=0 \] The difference with respect to GR is given by a nonvanishing function \(\delta(\eta)\). Several other modifications with respect to \(\mathrm{GR}\) are possible in the GW sector. The most immediate options are a deviation of the speed of GWs from the speed of light, or a graviton mass. Both would rather modify the \(c^{2} k^{2}\) term in above equation, but are now very significantly constrained: a deviation of the speed of GWs from the speed of light is excluded at the level \(\left|c_{\mathrm{gw}}-c\right| / c<\mathcal{O}\left(10^{-15}\right)\) by the observation of GW170817.
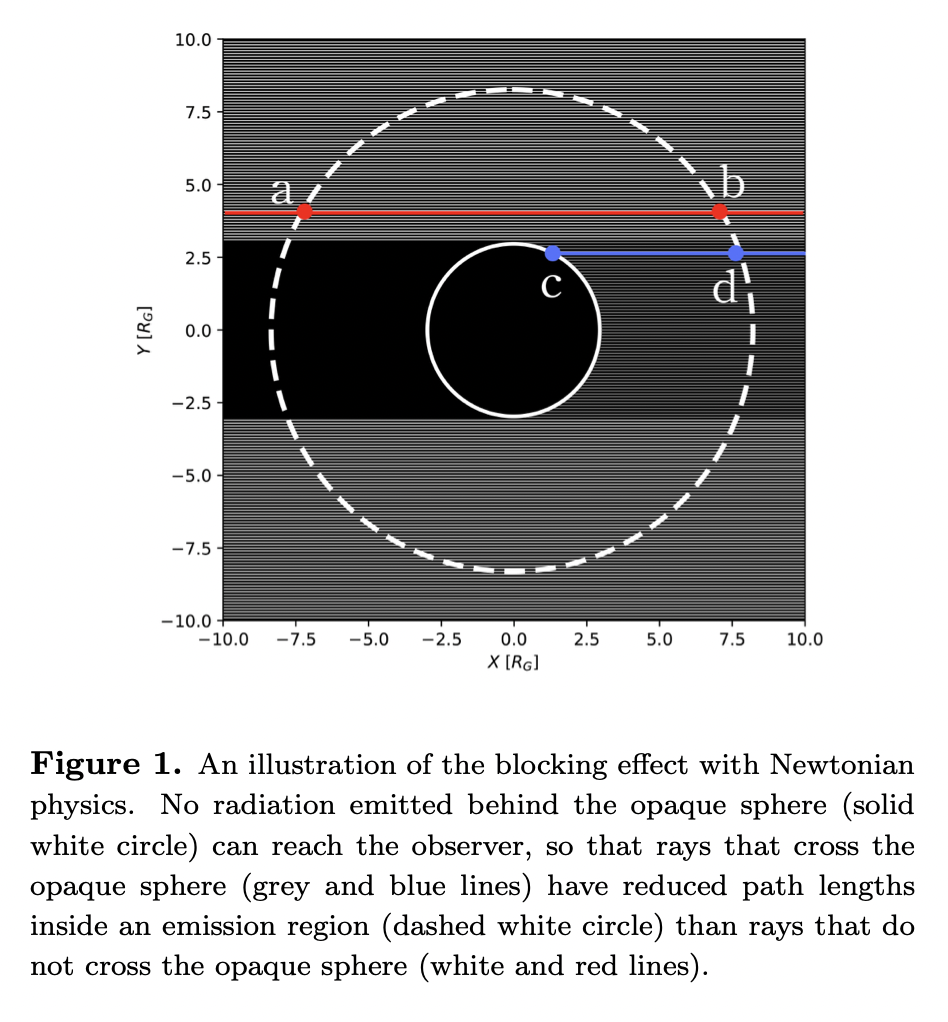
The Nature of Black Hole Shadows
This paper demonstrates that the black-hole shadow (the projection of a its unstable-photon region on an observer’s sky) is a distinct phenomenon from the photon ring.
In Newtonian physics, the observer's viewing rays travel along straight lines, and an observer image is constructed by solving the radiative transfer equation those rays: \[ \frac{d I_{\nu}}{d s}=j_{\nu}-\alpha_{\nu} I_{\nu} \] where \(j\) is the emission coefficient (which is constant in our simple model \(), I_{\nu}\) is the ray's specific intensity, and \(\alpha_{\nu}\) is the absorption coefficient (which is zero in this model).
Here defines a "darkening factor" \(\chi\) as the ratio of the intensities of the two rays as they reach the observer: \[ \chi_{\nu}=\frac{\int_{c}^{d} j_{\nu} d s+I_{\nu, \mathrm{sph}}}{\int_{a}^{b} j_{\nu} d s} \] where \(s\) parametrizes the integration distance along the rays, \(I_{\mathrm{sph}}\) is the specific intensity emitted by the sphere, and the position markers \(a, b, c, d\) are indicated in figure below. Note that \(\chi_{\nu}\) is frequency-dependent. Therefore, the cloud is observed at a frequency \(\nu\) at which it is optically thin.
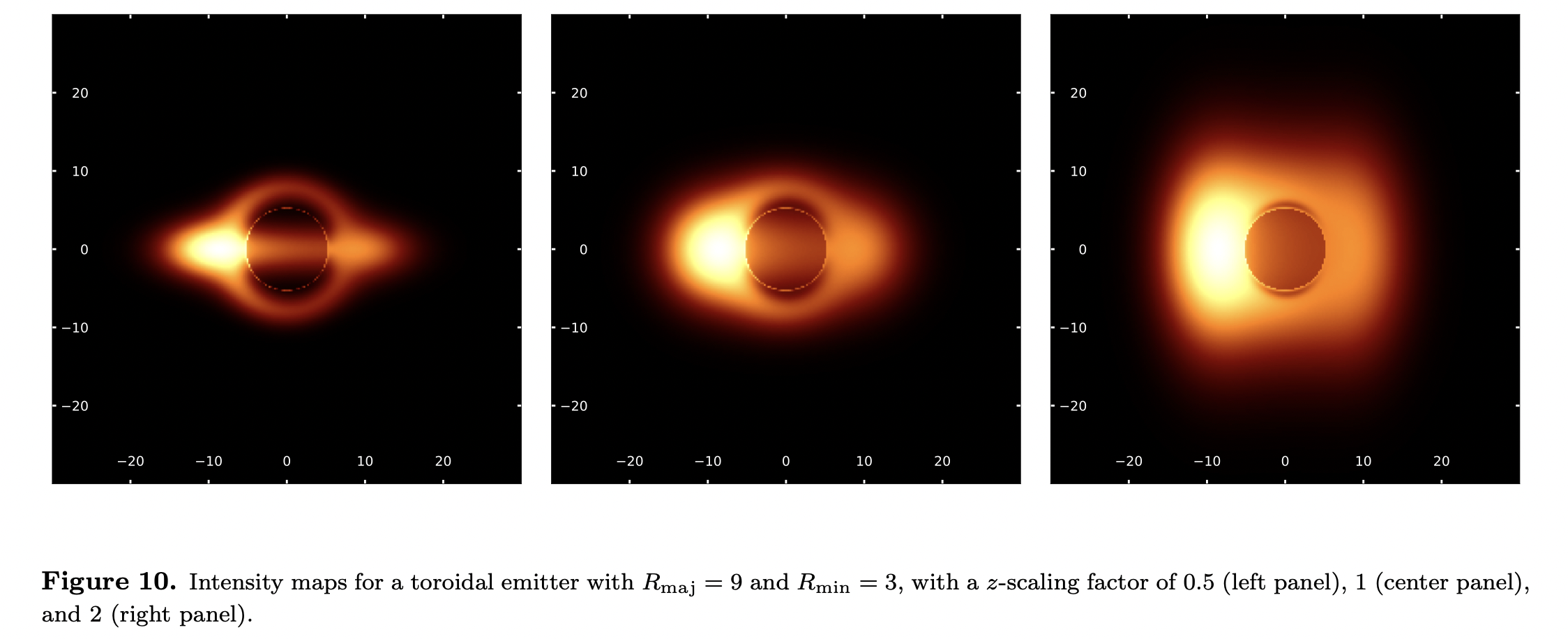
8-11
Tests for the existence of horizon through gravitational waves from a small binary in the vicinity of a massive object
Relativistic Generalized Uncertainty Principle and Its Implications
8-12
Basics of Apparent Horizons in Black Hole Physics
Gravitational time delay effects by Kerr and Kerr-Newman black holes in strong field limits
Detecting the Stochastic Gravitational Wave Background from Massive Gravity with Pulsar Timing Arrays
On the Angular Momentum Transport Efficiency within the Star Constrained from Gravitational-wave Observations
8-13
Investigating a New Approach to Quasinormal Modes: Physics-Informed Neural Networks
Constraining the orbital eccentricity of inspiralling compact binary systems with Advanced LIGO
Weak Gravity Decay of Rotating Extremal Black Holes
Formation of the First Two Black Hole - Neutron Star Mergers (GW200115 and GW200105) from Isolated Binary Evolution
- Using 560 BHNS binary population synthesis model realizations from Broekgaarden et al. (2021a), proving that the system properties (chirp mass, component masses and mass ratios) of both GW200115 and GW200105 match predictions from the isolated binary evolution channel. Concluding that the first two observed BHNS mergers can be explained from the isolated binary evolution channel for reasonable model realizations.
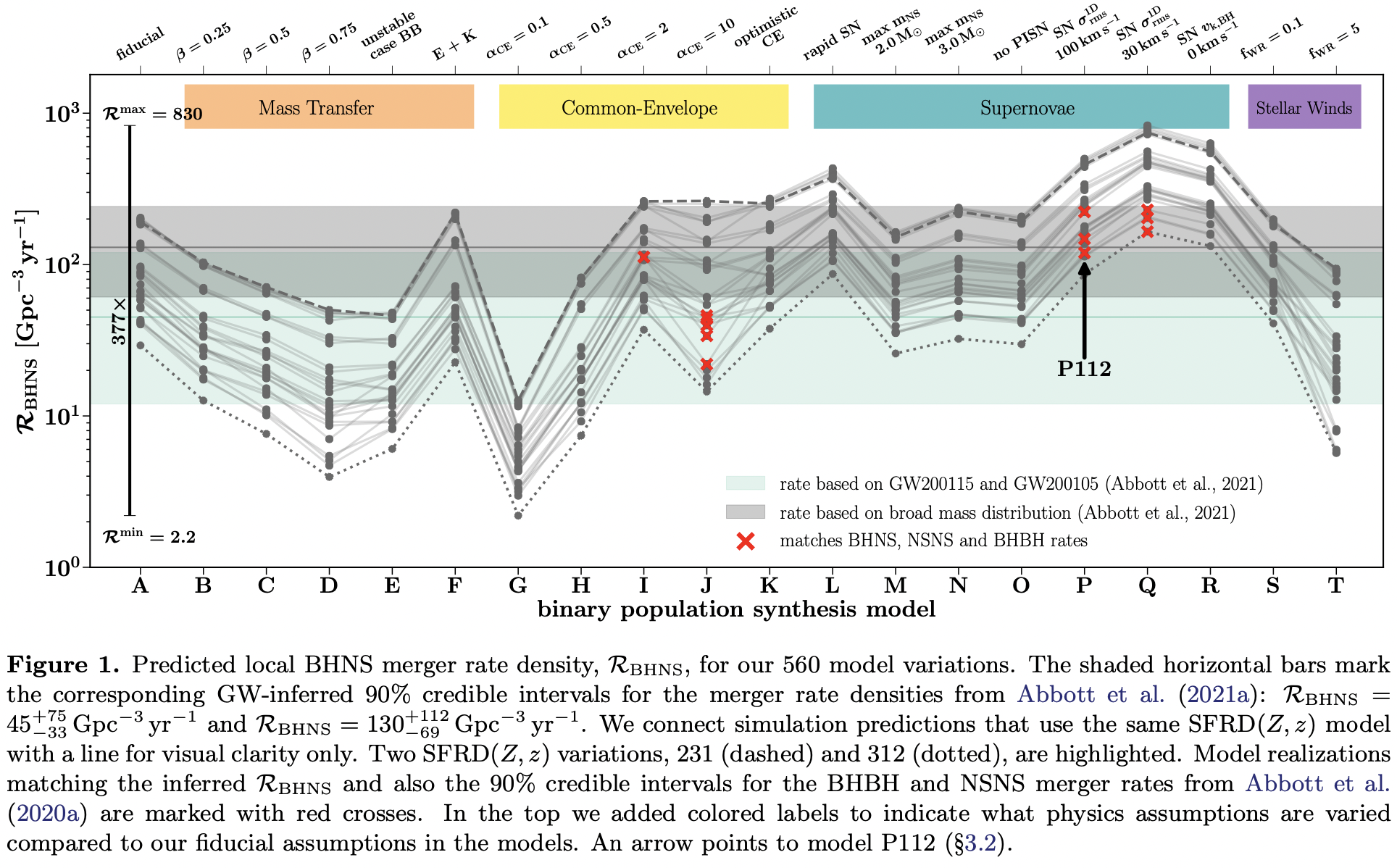
8-16
Analysis of birefringence and dispersion effects from spacetime-symmetry breaking in gravitational waves
8-18
Data-driven expectations for electromagnetic counterpart searches based on LIGO/Virgo public alerts
Presenting simulations of the next two LIGO/Virgo/KAGRA observing runs, O4 and O5, that are grounded in the statistics of O3 public alerts and study the follow-up strategy for the Zwicky Transient Facility.
This work highlights the need for timely observing scenarios that not only accurately reflect current understanding of the source properties and the detector network configurations, but also the S/N thresholds applied to public alerts. The authors recommend that future revisions of LRR use data-driven studies of GW alerts from past observing runs to verify that assumptions about S/N thresholds lead to realistic results, and promptly incorporate updated thresholds and public alert selection criteria into the official observing scenarios.
The rates and simulations encourage targeting smaller localizations from highly significant, nearby events for follow-up with deep observations.
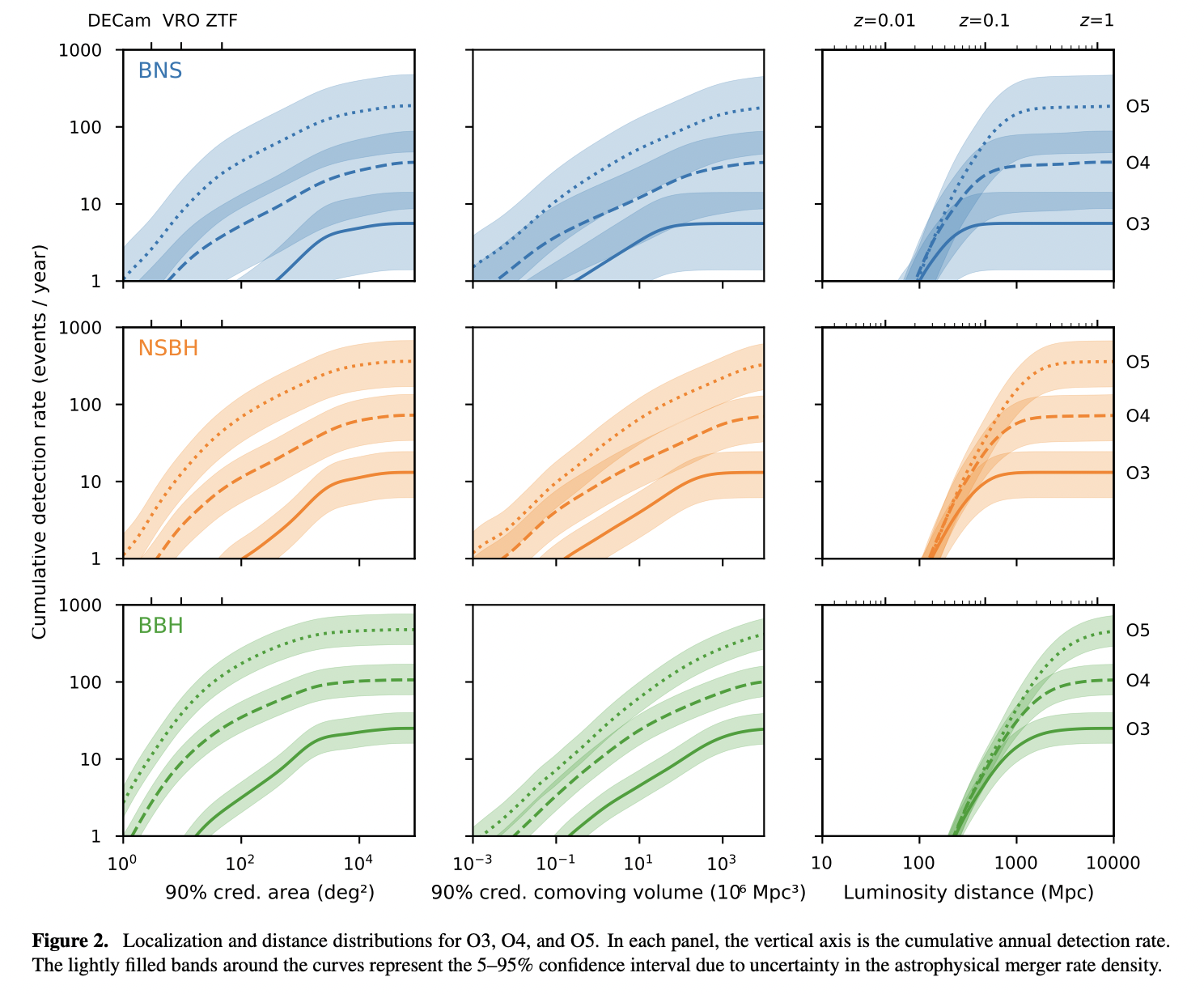
The double copy of the multipole expansion
The time traveler’s guide to the quantization of zero modes
8-20
The physics of non-ideal general relativistic magnetohydrodynamics
- This paper pays particular attention to the issue of local charge neutrality, which tends to be assumed but appears to be more involved than is generally appreciated. Highlights that the assumptions and simplifications may be tested by a new generation of models in simulations for relevant astrophysical scenarios.
Testing modified gravity with 21 cm intensity mapping, HI galaxy, cosmic microwave background, optical galaxy, weak lensing, galaxy clustering, type Ia supernovae and gravitational wave surveys
Neutron Star–Neutron Star and Neutron Star–Black Hole Mergers: Multiband Observations and Early Warnings
- Using the Fisher information matrix analysis to investigate the multiband synergy between the space-borne decihertz GW detectors and the ground-based Einstein Telescope (ET).
8-30
Fundamental Tone and Overtones of Quasinormal Modes in Ringdown Gravitational Waves: A Detailed Study in Black Hole Perturbation
- This paper performed numerical simulations of post-merger phase of binary black holes by using the black hole perturbation scheme with the initial data given under the post-Newtonian (PN) approximation, and generate data of ringdown gravitational waves with smaller numerical errors than that associated with currently available numerical relativity simulations.
September
9-7
Probing chromatic onsets of gravitational wave overtones
- Testing the assumptions used in previous analysis that first overtone and the fundamental mode were excited simultaneously by allowing different start times for them.
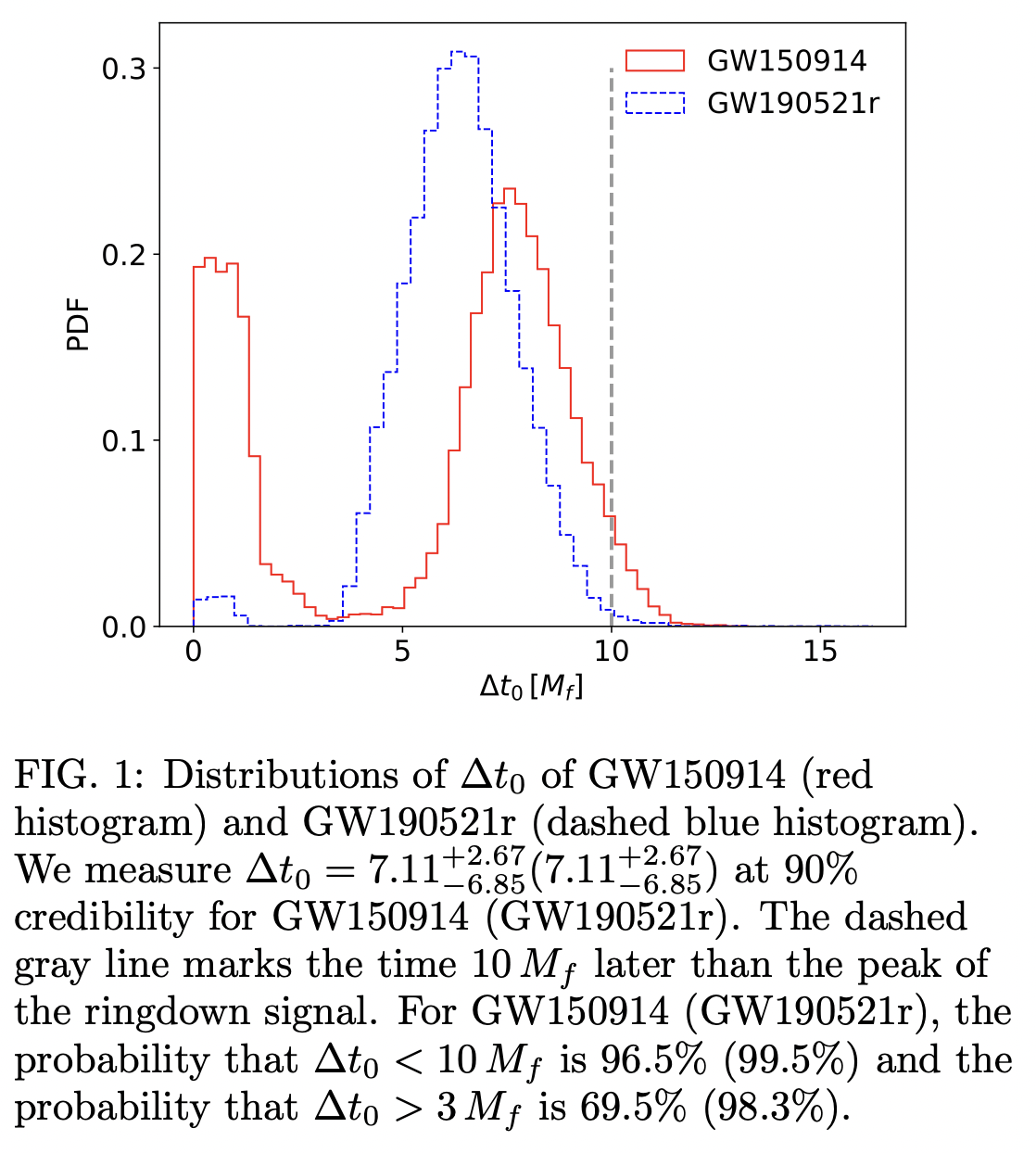
- The results indicated a clear chromatic onsets of the first overtone and the fundamental mode.
9-13
Conservative and radiative dynamics in classical relativistic scattering and bound systems
- A post-Minkowskian approach to the gravitational two-body problem. ompute for the first time the changes in linear momentum of each particle and the total radiated linear momentum, in the relativistic classical scattering of two point-charges, at sixth order in the charges (analogous to 3PM order in gravity).
9-14
Investigating the relation between gravitational wave tests of general relativity
Study of the relationship between several tests of GR using GW data. By implementing different simulated waveform with different extent of deviation to GR, the authors have found that while the larger deviation from GR is highly detecable, the smaller deviation from GR may be neglected.
The 5 tests that have been considered:
Residuals.
Reconstructions. \[ \mathcal{O}_{\mathrm{B}, \mathrm{L}}:=\frac{\left\langle\mathbf{h}_{L I} \mid \mathbf{h}_{\mathrm{BW}}\right\rangle}{\sqrt{\left\langle\mathbf{h}_{\mathrm{LI}} \mid \mathbf{h}_{\mathrm{LI}}\right\rangle\left\langle\mathbf{h}_{\mathrm{BW}} \mid \mathbf{h}_{\mathrm{BW}}\right\rangle}} \] where \(\langle\cdot \mid \cdot\rangle\) applied to boldface quantities indicates an inner product taken over the network, defined by: \[ \langle\mathbf{a} \mid \mathbf{b}\rangle:=\sum_{i=1}^{n} 4 \operatorname{Re} \int_{0}^{\infty} \frac{\tilde{a}^{i}(f) \tilde{b}^{i *}(f)}{S_{n}^{i}(f)} d f \]
IMR consistency test. \[ \begin{aligned} &\frac{\Delta M_{\mathrm{f}}}{\bar{M}_{\mathrm{f}}}:=2 \frac{M_{\mathrm{f}}^{\mathrm{insp}}-M_{\mathrm{f}}^{\text {postinsp }}}{M_{\mathrm{f}}^{\mathrm{insp}}+M_{\mathrm{f}}^{\mathrm{postinsp}}} \\ &\frac{\Delta \chi_{\mathrm{f}}}{\bar{\chi}_{\mathrm{f}}}:=2 \frac{\chi_{\mathrm{f}}^{\mathrm{insp}}-\chi_{\mathrm{f}}^{\mathrm{postinsp}}}{\chi_{\mathrm{f}}^{\mathrm{insp}}+\chi_{\mathrm{f}}^{\mathrm{postinsp}}} \end{aligned} \] where the "insp" and "postinsp" superscripts denote the estimates obtained from the inspiral and postinspiral portions of the signal. These fractional deviations should be consistent with zero if the waveform model is a good description of the observed signal.
Parameterized tests of gravitational-wave generation.
- One version of the parametrized test is the Test Infrastructure for GEneral Relativity (TIGER) approach [1, 2, 3], whose implementation applied to LIGO-Virgo detections to date uses IMRPhenomPv2 as the underlying GR model.
- A second approach is the Flexible Theory-Agnostic (FTA) approach, which is not tied to a specific waveform model, but only considers the inspiral PN coefficients.
Modified dispersion test.
Certain alternative theories of gravity predict a massive graviton and thus dispersion effects as the waves travel from the source to the observer. \[ E^{2}=p^{2} c^{2}+A_{\alpha} p^{\alpha} c^{\alpha} \] Here \(A_{\alpha}\) is the amplitude of the modified dispersion (zero in GR) and has dimension of [Energy] \(^{2-\alpha} ; \alpha\) is a dimensionless constant. In particular, \(\alpha=0\) and \(A_{0}>0\) corresponds to a massive graviton with mass \(m_{\mathrm{g}}=A_{0}^{1 / 2} / c^{2} .\)
9-20
On the ease of excitation of black hole ringing: Quantifying the importance of overtones by the excitation factors
Cosmologically coupled compact objects: a single parameter model for LIGO–Virgo mass and redshift distributions
This paper develops a single-parameter route for reproducing higher mass objects as observed in the LIGO–Virgo mass distribution, using only the isolated binary stellar evolution channel, which encodes the cosmological mass growth of compact stellar remnants that exceed the Tolman-Oppenheimer-Volkoff limit.
This paper adopted the following single parameter model of cosmological coupling: \[ m(a):=m_{0}\left(\frac{a}{a_{i}}\right)^{k} \quad a \geqslant a_{i} \] Here \(m_{0}\) is the active gravitational mass of the input stellar remnant, \(a\) is the scale factor, \(a_{i}\) is the scale factor at which the input stellar remnant was formed, and \(k\) is a dimensionless constant. This form is motivated by the known cosmological energy shift in photons \((k=\) -1), and the predicted cosmological energy shift in pure Dark Energy objects \((k=3)\). Note that \(k \rightarrow 0\) is the decoupled limit, \(k<0\) gives a cosomological energy loss, and \(k>0\) gives a cosmological energy gain. From global analysis, physically realistic values of \(k\) are constrained to: \[ -3 \leqslant k \leqslant 3 \] by the requirement that all causal observers perceive causal flux.
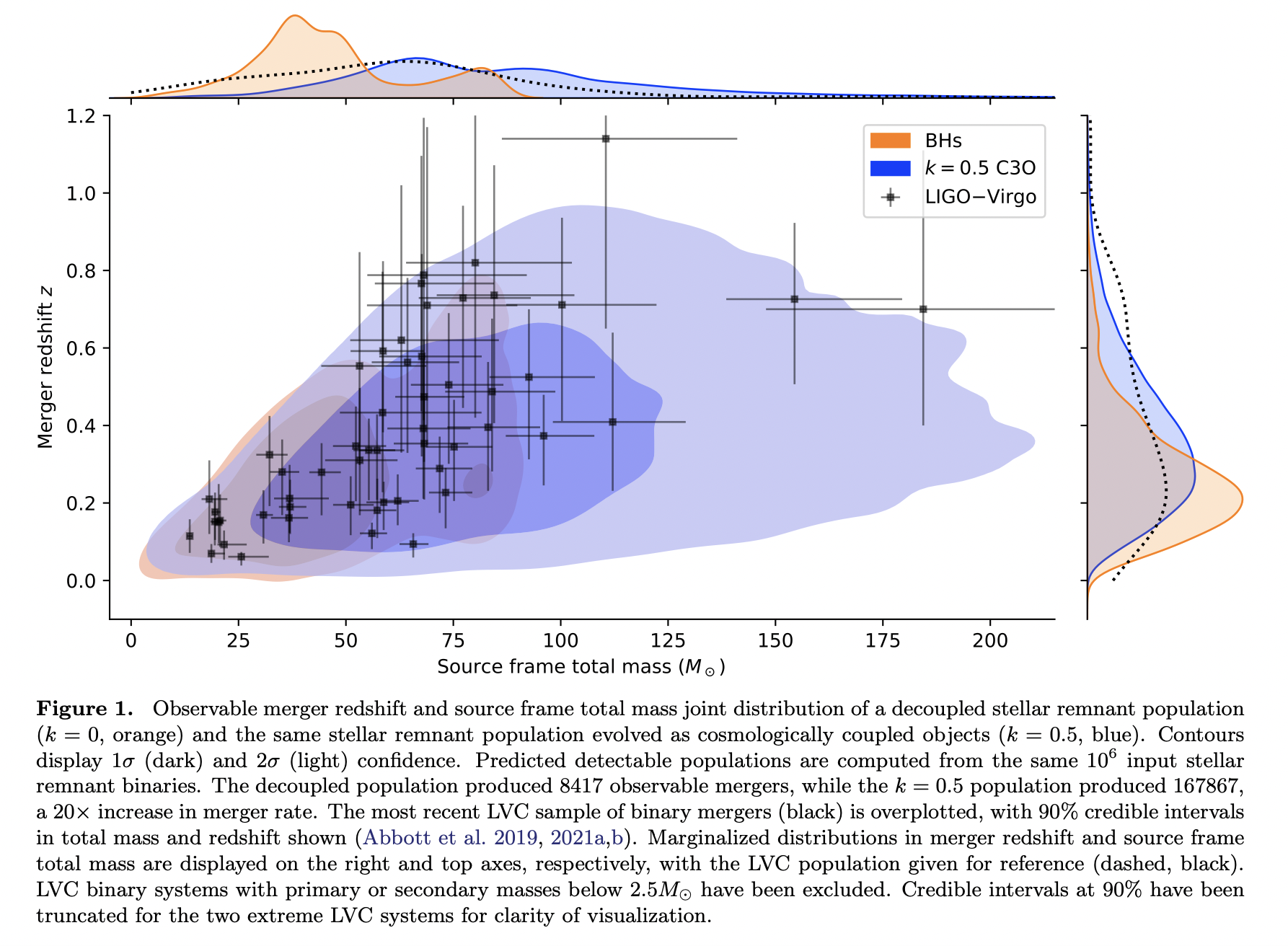
9-21
Deformed Schwarzschild horizons in second-order perturbation theory
Recent years' GW observation has enabled more detailed analyses of the dynamical black holes in these systems. This paper derived generic formulas for the first- and second-order perturbative corrections to the radial profiles, surface areas, Hawking masses, and intrinsic curvatures of a perturbed Schwarzschild black hole’s apparent and event horizon.
The two horizons are identical at linear order regardless of the source of perturbation, but do generically differ at second order.
Constraining cosmological extra dimensions with gravitational wave standard sirens: from theory to current and future multi-messenger observations
By assuming that gravity propagates through the higher-dimensional spacetime, while photons are constrained to the usual four dimensions of general relativity, this paper derived from first principles the relation between the luminosity distance measured by GW detectors and the one inferred by EM observations.
This paper extends and updates previous analyses which crucially neglected an additional redshift dependency in the GW-EM luminosity distance relation which affects results obtained from multi-messenger GW events at high redshift, in particular constraints expected from LISA MBHBs.
\[ d_{L}^{\mathrm{GW}}=d_{L}^{\mathrm{EM}}\left[1+\left(\frac{d_{L}^{\mathrm{EM}}}{R_{c}(1+z)}\right)^{n}\right]^{(D-4) /(2 n)} \]
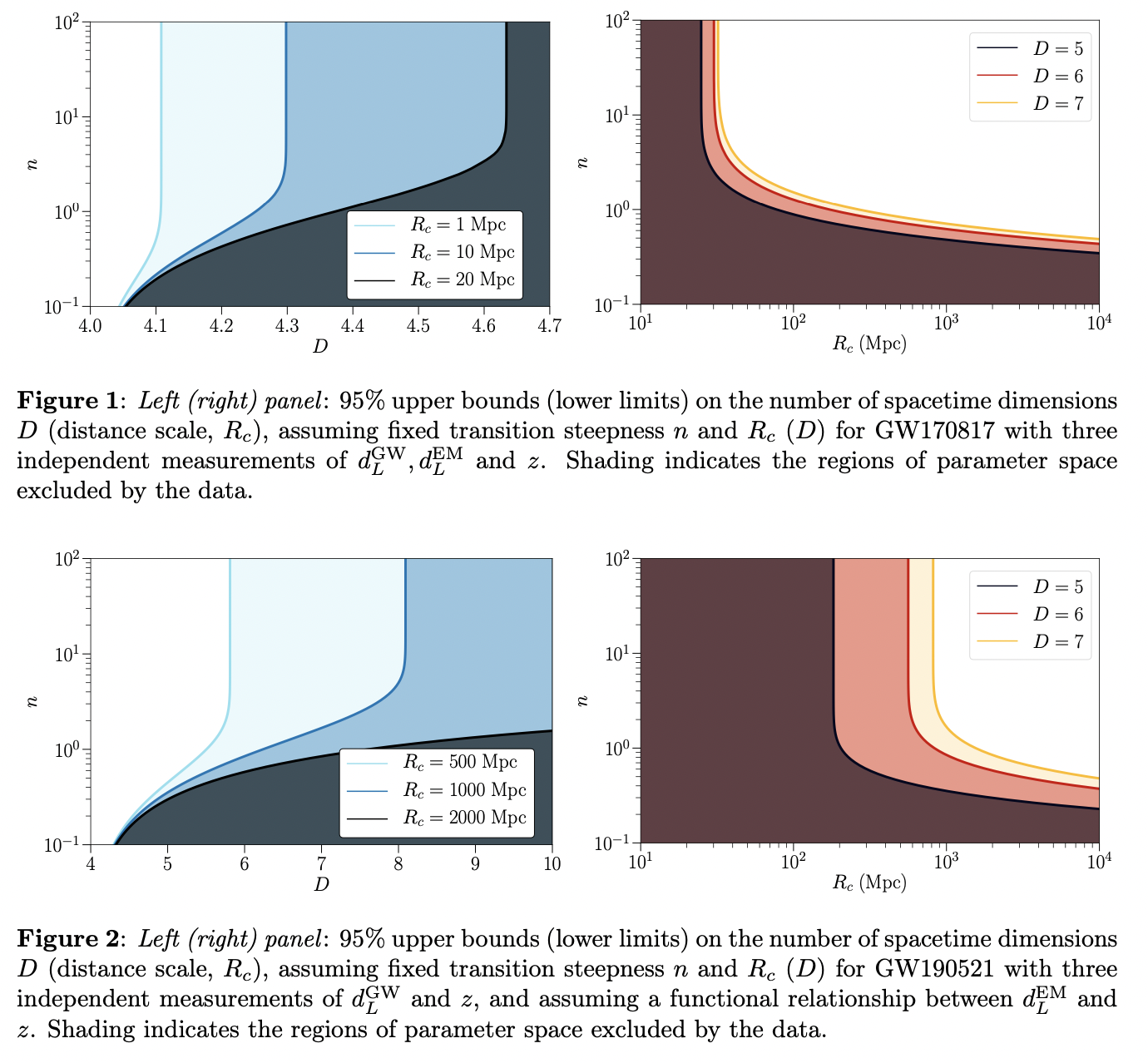
LISA will be able to distinguish between ΛCDM and a 5-dimensional cosmological model irrespective of the underlying astrophysical properties of the MBHB population.
In fact from our analysis it is clear that current LIGO/Virgo results, in particular GW170817, can only constrain Rc up to tens of Mpc, while LISA will allow us to push constraints up to Gpc scales with the detection of MBHB mergers.
Tests of Gravitational-Wave Birefringence with the Gravitational-Wave Catalog
Finding an outlier, GW190521, that supports the existence of birefringence over general relativity with a higher match-filtering signal-to-noise ratio and a natural log Bayes factor of 7.84.
Birefringence, an effect where the left- and right-handed polarizations of gravitational waves follow different equations of motion, occurs when the parity symmetry of gravity is broken.
In GW data analysis, the parity-violating waveform in frequency domain is: \[ \begin{aligned} &h_{+}^{\mathrm{PV}}(f)=h_{+}^{\mathrm{GR}}(f)+h_{\times}^{\mathrm{GR}}(f) \delta \Psi \\ &h_{\times}^{\mathrm{PV}}(f)=h_{\times}^{\mathrm{GR}}(f)-h_{+}^{\mathrm{GR}}(f) \delta \Psi \end{aligned} \] The phase modification to the GR-based waveform \(h^{\mathrm{GR}}(f)\) takes the following form \[ \delta \Psi(f)=\frac{(\pi f)^{2}}{M_{\mathrm{PV}}} \int_{0}^{z} \frac{\alpha_{\mu}\left(z^{\prime}\right)\left(1+z^{\prime}\right) d z^{\prime}}{H_{0} \sqrt{\Omega_{M}\left(1+z^{\prime}\right)^{3}+\Omega_{\Lambda}}} \]
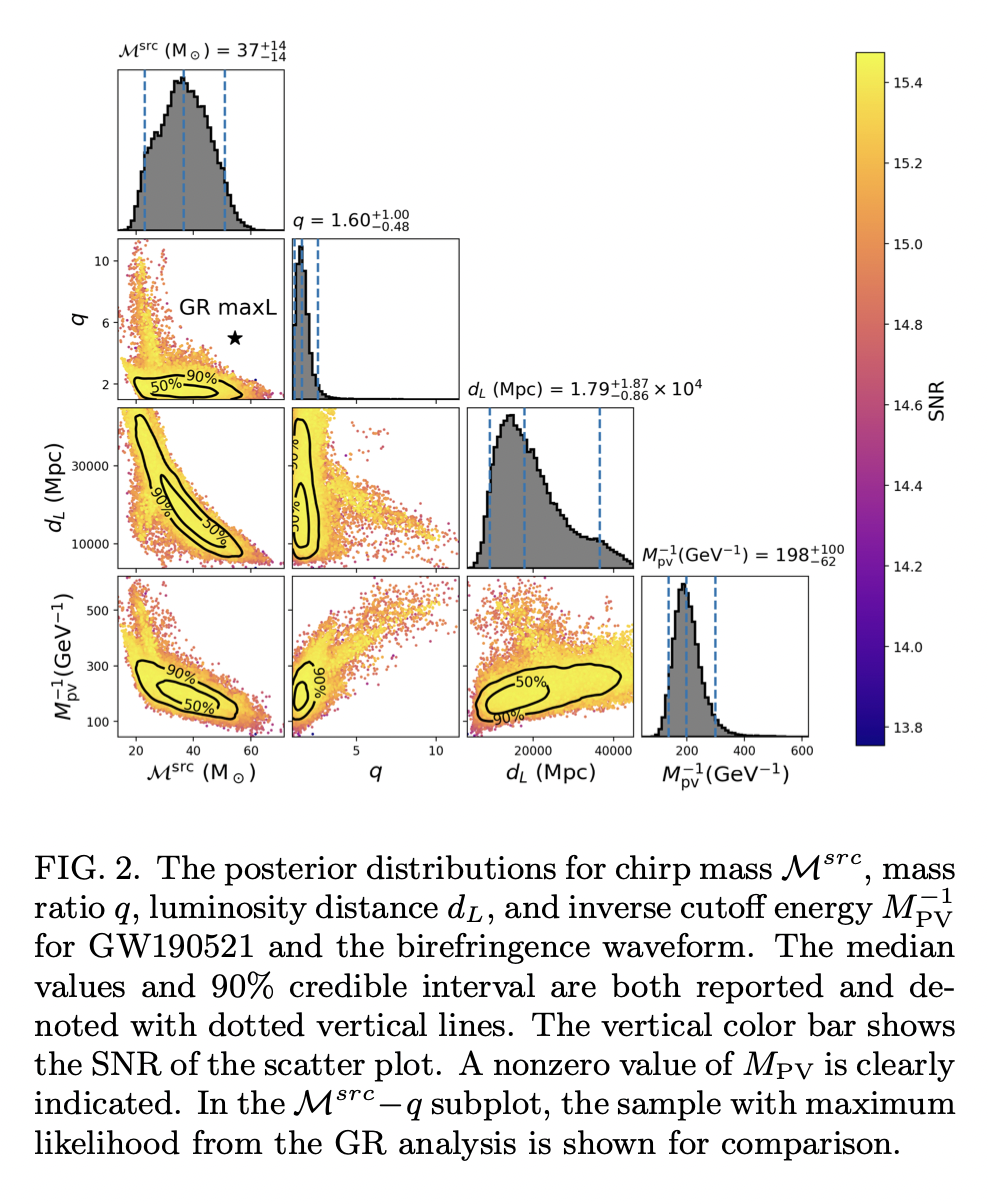
The author hypothesized that the result may be caused by the limitations of the existing waveform approximants, such as systematic errors during merger phase of the waveform, or by the existence of physical effects such as eccentricity which are not taken into account by the current waveform approximants.
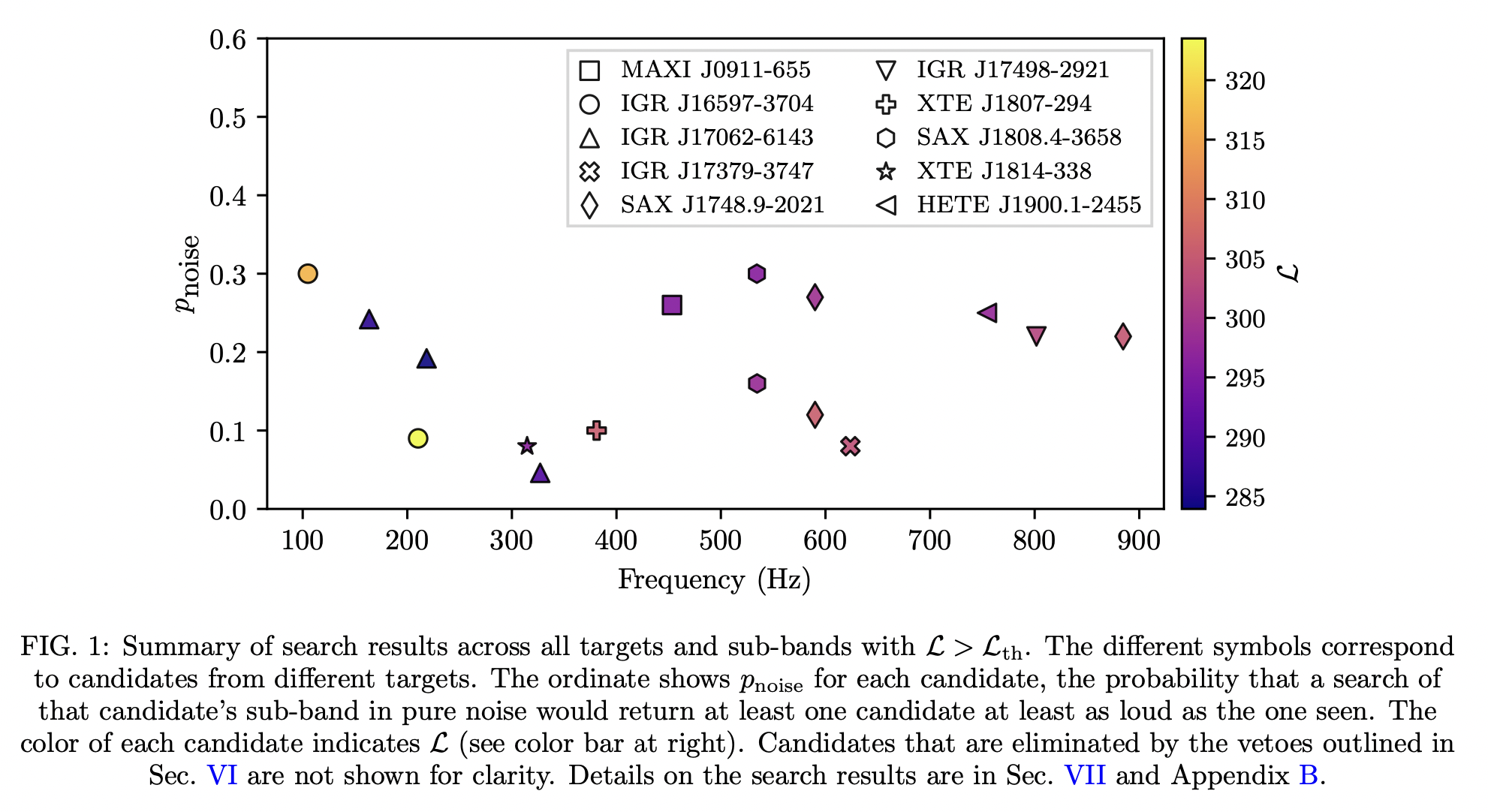
Search for continuous gravitational waves from 20 accreting millisecond X-ray pulsars in O3 LIGO data
- The search algorithm uses a hidden Markov model to find continuous gravitational waves from accreting millisecond X-ray pulsars. No candidates were found that survive the veto procedure and are above a threshold corresponding to a 1% false alarm probability per sub-band, only 16 of them survived the 30% false alarm probability.
- The paper used three of the vetoes from Ref. [12]:
- Known line veto
- Single interferometer veto
- Off-target veto
9-22
Distinguishing modified gravity with just two tensorial degrees of freedom from general relativity: Black holes, cosmology, and matter coupling
Quasi-normal modes and Microscopic Structure of the Schwarzschild Black Hole
9-24
Observationally driven Galactic double white dwarf population for LISA
9-28
Splitting the third hair: constraints on Kerr-Newman black holes from merger-ringdown gravitational-wave observations
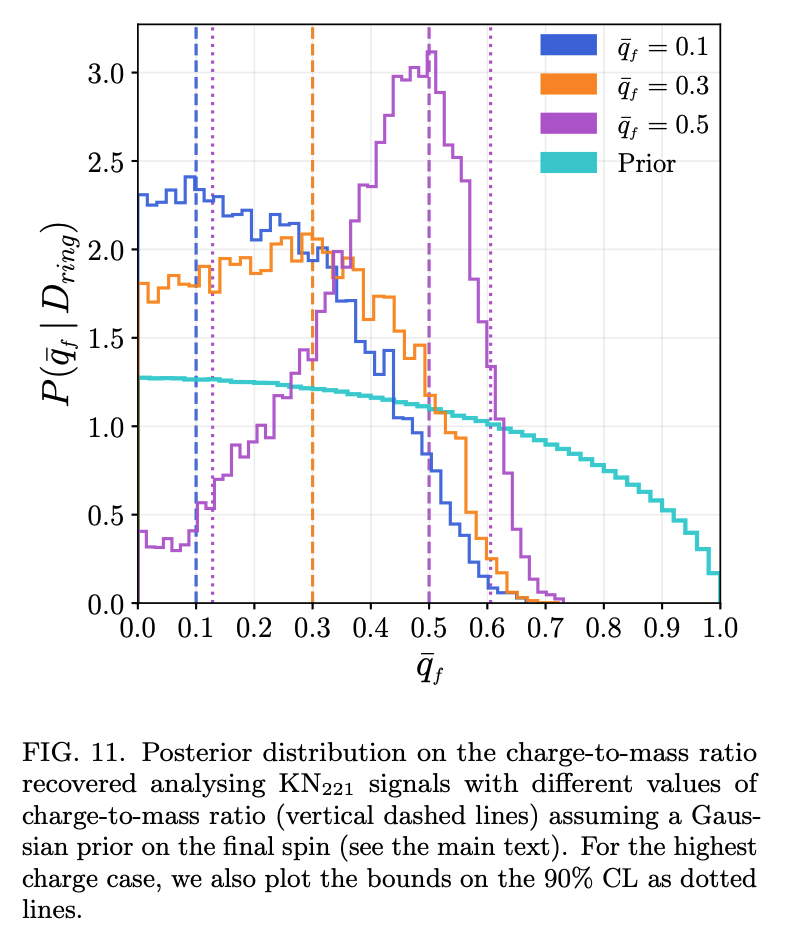
Calculate the quasi-normal mode complex frequencies of the Kerr-Newman black hole with arbitrary values of spin and charge, for the modes typically dominant during a binary black hole coalescence, \((\ell, m, n)=\{(2,2,0),(2,2,1),(3,3,0)\}\). Aside from astrophysical electric charge, this template can accommodate extensions of the Standard Model, such as a dark photon. Obtain a 90th percentile bound \(\bar{q}<0.33\) on the black hole charge-to-mass ratio, for the most favorable case of GW150914. However, this model can only provide a robust measurement of the charge-to-mass ratio only for values \(\bar{q}>0.5\). Thus, this result should instead be detected when evaluating the consistency of the pre-merger and post-merger emission.
Multi-band gravitational wave cosmology with stellar origin black hole binaries
October
10-1
GW200115: A NON-SPINNING BLACK HOLE – NEUTRON STAR MERGER
10-7
Angular emission patterns of remnant black holes
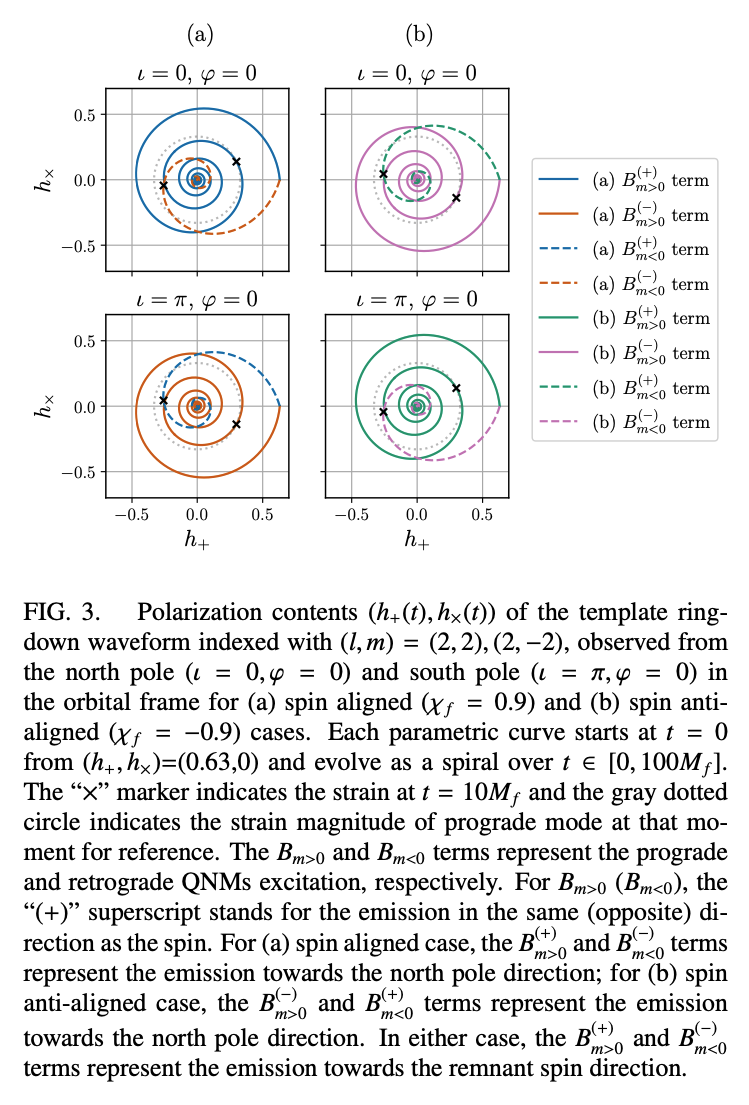
Study the spatial distribution og the ringdown emission. Specifically, when the final spin is not aligned with the initial orbital angular momentum, the spatial properties for retrograde excitations have not been carefully studied. Show that spin-weighted spheroidal harmonics are the better representation of the ringdown angular emission patterns compared to spin- weighted spherical harmonics in fits to numerical relativity waveforms.
Spatial dependence.- For prograde (retrograde) modes with indices \(m>0(m<0)\), the \(\left\{B_{l m n}^{(S+)}{ }_{-2} S_{l m n}\left(\gamma_{l m n}, \tilde{\iota}, \tilde{\varphi}\right)\right\}\), \(\left\{B_{l m n}^{(Y+)}-2 Y_{l m}(\tilde{\imath}, \tilde{\varphi})\right\}\) terms describe the emission mainly towards the north (south) hemisphere, while the \(\left\{B_{l m n}^{(S-)}-2 S_{l m n}^{*}\left(\gamma_{l m n}, \pi-\right.\right.\) \(\tilde{\iota}, \tilde{\varphi})\},\left\{B_{l m n}^{(Y-)}-2 Y_{l m}^{*}(\pi-\tilde{\imath}, \tilde{\varphi})\right\}\) ones describe the emission mainly towards the south (north) hemisphere. The coefficients \(B_{l m n}^{(S \pm / Y \pm)}\) are the corresponding excitations of the \(l m n\) mode and are governed by the merging dynamics of the progenitor binary. The temporal and spatial features of different terms are summarized in the table below:

where the Ref. [67] is Berti's paper.
10-12
A nonparametric method to assess significance of events in search for gravitational waves with false discovery rate
10-19
RUNMON-RIFT: Adaptive Configuration and Healing for Large-Scale Parameter Inference
- For one parameter inference pipeline--RIFT, the authors have developed a flexible tool (RUNMON-RIFT) to mitigate the most common challenges introduced by two types of uncertainties: i) data containing unknown sources, ii) distributed hardware with unreliable performance. On the one hand, RUNMON provides several mechanisms to identify and redress unreliable computing environments. On the other hand, RUNMON provides mechanisms to adjust pipeline-specific run settings, including prior ranges, to ensure the analysis completes and encompasses the physical source parameters.
10-27
Multi-messenger Time-domain Signatures Of Supermassive Black Hole Binaries
10-28
Metric Assisted Stochastic Sampling (MASS) search for gravitational waves from binary black hole mergers
- Present a novel gravitational wave detection algorithm that conducts a matched filter search stochastically across the compact binary parameter space rather than relying on a fixed bank of template waveforms. Using approximately one month of public LIGO data from July 27 00:00 2017 UTC – Aug 25 22:00 2017 UTC and recover seven known confident gravitational wave candidates as well as injecting simulated binary black hole (BBH) signals to demonstrate the sensitivity.
10-29
High Precision Ringdown Modeling: Multimode Fits and BMS Frames
November
11-2
Applying higher-modes consistency test on GW190814 : lessons on no-hair theorem, nature of the secondary compact object and waveform modeling
11-3
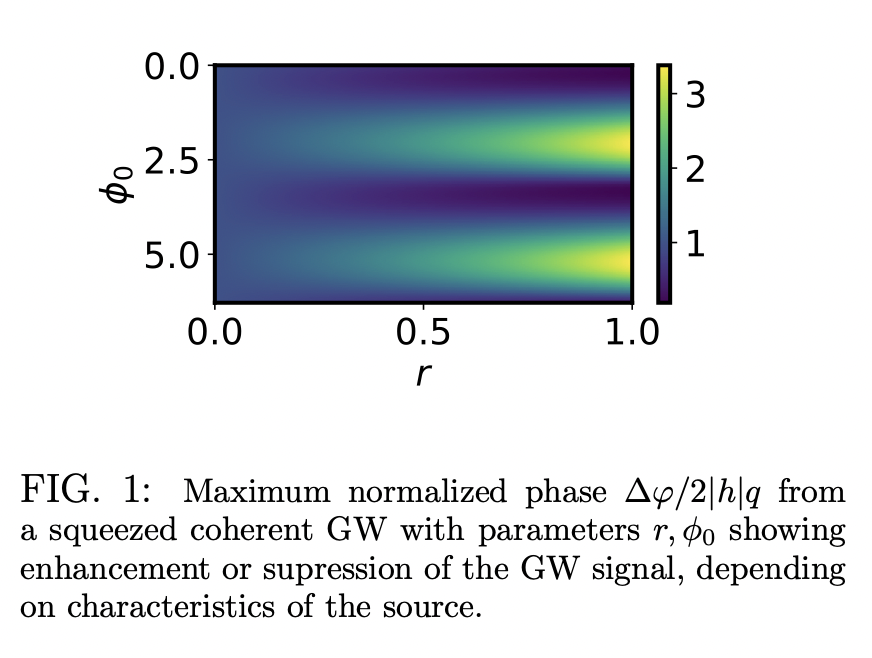
Quantum Signatures in Nonlinear Gravitational Waves
Squeezed-coherent gravitational waves can enhance or suppress the signal measured by an interferometer, which is a characteristic effect of quantum optics. Detection of such an enhanced or suppressed signal would be evidence for the quantum nature of gravitational waves. This paper has presented a proof-of-principle for the amplification and suppression of GW signals due to squeezed-coherent GWs.
The interaction reads: \[ H_{I}=-\frac{\omega}{4} a^{\dagger} a \int \frac{d \boldsymbol{k}}{\sqrt{(2 \pi)^{3}}}\left(\sqrt{\frac{8 \pi G}{k}} \mathfrak{b}_{\boldsymbol{k}}+\text { h.c. }\right) \] where \(k=|\boldsymbol{k}|=\Omega_{k}\) is the GW frequency for mode \(\boldsymbol{k}, \mathfrak{b}_{k}^{\lambda}\left(\mathfrak{b}_{k}^{\lambda \dagger}\right)\) is the canonical graviton annihilation (creation) operator and \(\omega\) is the cavity frequency. Following the standard procedure in quantum optics, a quantization volume \(V\) is introduced and note that \([\sqrt{8 \pi G / k}]=L^{3 / 2}\), where \(L\) denotes the dimension of length. Further, \([d \boldsymbol{k}]=L^{-3}\).
We can write a general effective Hamiltonian governing the four-graviton helicity preserving process: \[ H_{g, g}=\mathcal{N} \frac{G}{V}\left(b_{1}^{\dagger} b_{2}^{\dagger} c d+\text { h.c. }\right) \] where \(\mathcal{N}\) is a dimensionless kinematic factor roughly of order unity whose exact value is not relevant for the estimate, \(c, d\) are the graviton annihilation operators for the incoming modes, \(b_{1}^{\dagger}, b_{2}^{\dagger}\) are the creation operators for the outgoing GWs, and \(V\) is the quantization volume as defined previously.
If we consider the interaction length to be just above the Schwarzschild radius of the black holes, say twice as big, \(\ell \sim 4 G M / c^{2}\), the squeezing parameter reads: \[ r \sim \frac{\mathcal{N}}{32 \pi}\left(\frac{c^{3}}{G M}\right) \times \frac{\left(\frac{4 G M}{c^{2}}\right)}{c} \times f^{2}=\frac{\mathcal{N} f^{2}}{8 \pi} \]
11-4
Apples and Oranges: Comparing black holes in X-ray binaries and gravitational-wave sources
11-5
GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo During the Second Part of the Third Observing Run
11-9
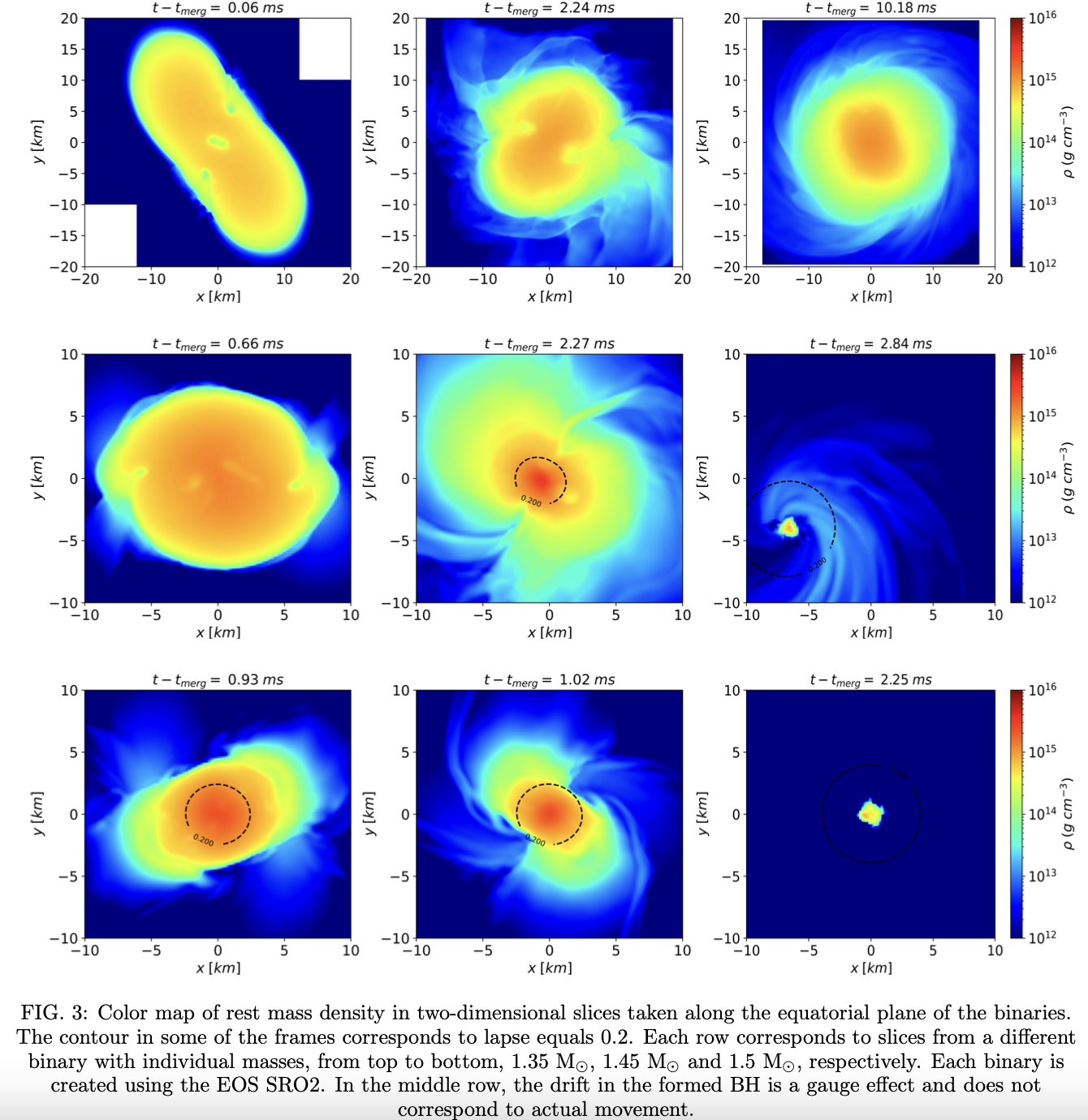
Numerical relativity simulations of prompt collapse mergers: threshold mass and phenomenological constraints on neutron star properties after GW170817
- Attempt to determine the threshold mass for prompt (no bounce) black hole formation in equal-mass neutron star (NS) mergers using a new set of 227 numerical relativity simulations. While considering 23 phenomenological and microphysical finite temperature equations of state (EOS), including models with hyperons and first-order phase transitions to deconfined quarks, this work introduces new methods to constrain the upper as well as lower limit of NS maximum mass using future BNS detections and their identification as prompt or delayed collapse.
11-10
Pulsar-timing measurement of the circular polarization of the stochastic gravitational-wave background
- This work addresses the circular polarization of the SGWB by isolating the real and imaginary parts of the timing residual correlation. After construct an estimator that can naturally distinguish between the intensity and circular polarization contributions of the SGWB, which is based on extracting the real and imaginary parts of the cross-correlation between pulsar timing residuals, they compute the optimal filter and the combination of pulsar pairs that maximizes the signal-to-noise ratio of the circular polarization component.
11-12
Radiation hydrodynamics modeling of kilonovae with SNEC
- The paper develops a method to compute synthetic kilonova light curves that combines numerical relativity simulations of neutron star mergers and the SNEC radiation-hydrodynamics code, which implement the initial and boundary conditions, r- process heating, and opacities for kilonova simulations. None of models tested match AT2017gfo, the kilonova in GW170817. This points to possible deficiencies in the merger simulations and to the need to go beyond the assumption of spherical symmetry adopted in this work.
- SNEC: the SuperNova Explosion Code, is a spherically symmetric (1D) Lagrangian radiation-hydrodynamics code, primarily used to simulate core-collapse supernova explosions and generate synthetic color light curves
Gravitational-Wave Data Analysis: Computing Challenges in the 3G Era
Future Ground-Based Gravitational-Wave Observatories: Synergies with Other Scientific Communities
The Next Generation Global Gravitational Wave Observatory
11-14
M2 thesis: Effective Field Theory for Gravitational Radiation in General Relativity and beyond
- Study the conservative and dissipative dynamics of binary systems of compact objects in the post-Newtonian expansion. The first part reviews a binary of non-spinning black holes at leading post-Newtonian order. The second part presents the so-called Kaluza-Klein parametrization of the metric, then extend this parametrization to (conformally-coupled) scalar-tensor gravity.
A scalable elliptic solver with task-based parallelism for the SpECTRE numerical relativity code
- XCTS equations
11-16
Notes on primordial black hole origin for thermal gamma-ray bursts
Demonstrate the flaws in one scenario: Hawking radiation emitted from a PBH freely falling into a more massive BH could produce thermal gamma-ray burst. In particular, the rate of occurrence of PBH-BH mergers is predicted to be far lower than the reciprocal age of the universe, and the predicted radiance observed from Earth is found to be orders of magnitude lower than what any instrument could detect.
are typically characterized by non-thermal spectra, and despite the diversity in their light curves and the uncertainty in their exact emission mechanisms, the sources for GRBs are almost unanimously agreed upon to fall under two classes, based on the GRB’s duration:
- Short GRBs, with a duration of tenths of a second, are associated with kilonovae produced from compact binary mergers. For example, the detection of the short GRB 170817A alongside LIGO’s detection of gravitational wave GW170817 from a neutron star merger event.
- Long GRBs, with a duration of tens of seconds, are result from massive stars undergoing core-collapse.
For a blackbody emitter, the spectral radiance is given by Planck's law: \[ I_{\omega^{\prime}}=\frac{\omega^{\prime 3}}{2 \pi^{2}\left(\mathrm{e}^{\omega^{\prime} / T^{\prime}}-1\right)} \] where the Hawking temperature \(T^{\prime}\) emitted in the PBH's rest frame is assumed to be constant over the duration of the free fall event: \[ T^{\prime}=\frac{1}{8 \pi M_{\mathrm{e}}} \]
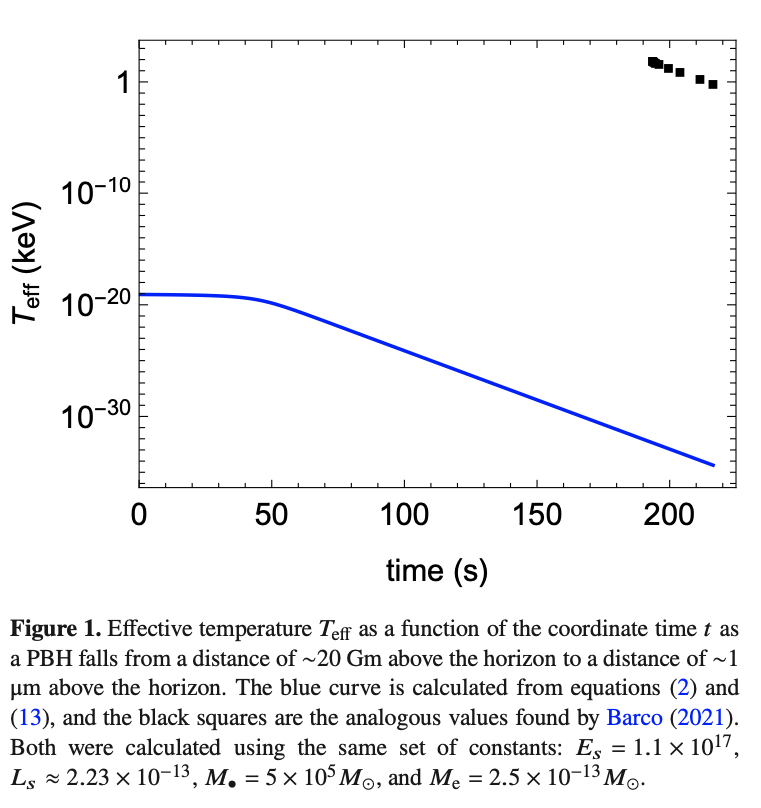
11-17
An improved numerical fit to the peak harmonic gravitational wave frequency emitted by an eccentric binary
Present the numerical fit to the peak harmonic gravitational wave (GW) frequency emitted by an eccentric binary system in the post-Newtonian approximation, which significantly improves the previous fit particularly for eccentricities \(\lesssim 0.8\) cases. The new fit should be useful for future studies of eccentric sources.
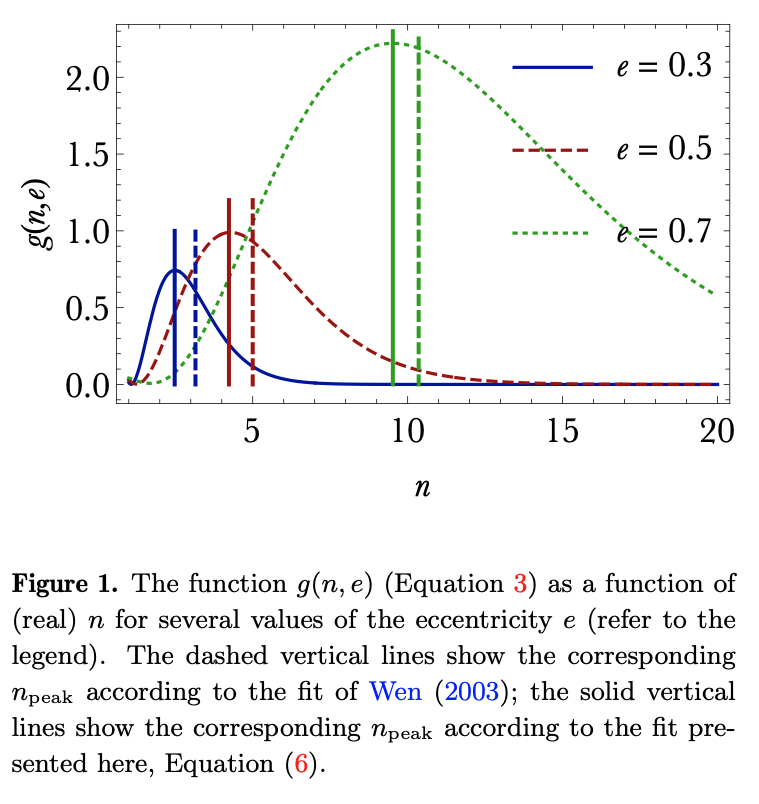
As shown in the seminal work of Peters & Mathews (1963) that assumed the post-Newtonian approximation, an eccentric binary (eccentricity \(e\) ) emits GWs at additional harmonics. Specifically, the power of the \(n^{\text {th }}\) harmonic with frequency \(f_{\mathrm{GW}, n}=n f_{\text {orb }}\) (with integer \(n \geq 1\) ) is given by \[ P_{n}=\frac{32}{5} \frac{G^{4}}{c^{5}} \frac{m_{1}^{2} m_{2}^{2} M}{a^{5}} g(n, e) \] where the function \(g(n, e)\) quantifies the factor to which more power is emitted in the \(n^{\text {th }}\) harmonic compared to a circular orbit. The latter function is given by \[ \begin{aligned} &g(n, e)=\frac{n^{4}}{32}\left\{\left[J_{n-2}(n e)-2 e J_{n-1}(n e)+\frac{2}{n} J_{n}(n e)\right.\right. \\ &\left.\quad+2 e J_{n+1}(n e)-J_{n+2}(n e)\right]^{2}+\left(1-e^{2}\right)\left[J_{n-2}(n e)\right. \\ &\left.\left.\quad-2 J_{n}(n e)+J_{n+2}(n e)\right]^{2}+\frac{4}{3 n^{2}} J_{n}(n e)^{2}\right\} \end{aligned} \] where \(J_{i}(x)\) is the \(i^{\text {th }}\) Bessel function of the first kind. Fig. 1 plots \(g(n, e)\) as a function of \(n\) (interpreted as a real number for the purposes of plotting) for several values of the eccentricity \(e\). More eccentric binaries typically emit more power at higher harmonics.
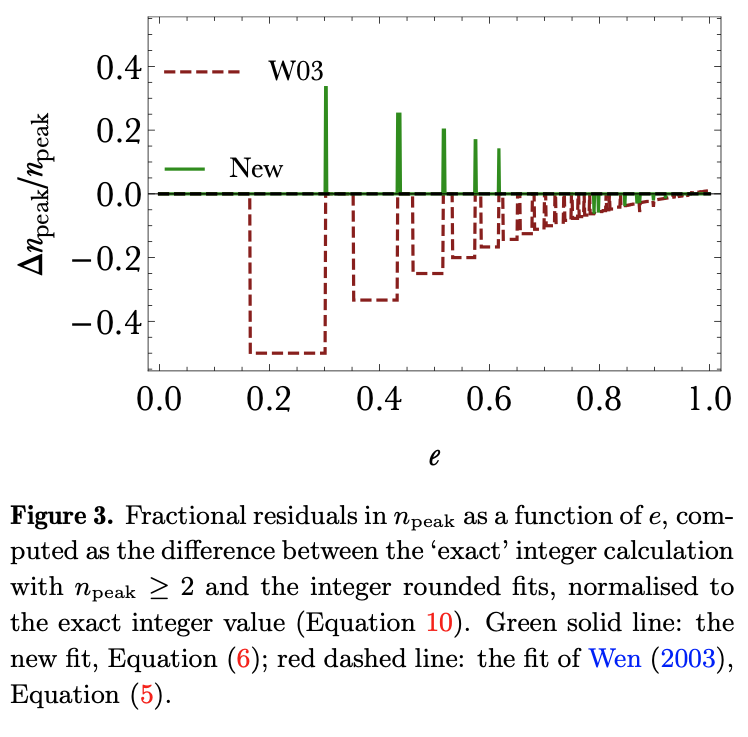
Lastly, the arthor shows the below figure as a function of \(e\) the fractional residuals in the integer \(n_{\text {peak }}\) computed as the difference between the 'exact' integer-rounded calculation with \(n_{\text {peak }} \geq 2\) and the integer-rounded fits, i.e., \[ \frac{\Delta n_{\text {peak }}}{n_{\text {peak }}}=\frac{\operatorname{int}\left[n_{\text {peak }}^{\text {(exact) }}\right]-\operatorname{int}\left[n_{\text {peak }}^{\text {(fit) }}\right]}{\operatorname{int}\left[n_{\text {peak }}^{(\text {exact })}\right]} \] For \(e \lesssim 0.8\), the fit of Wen (2003) systematically overpredicts \(n_{\text {peak }}\left(\Delta n_{\text {peak }}<0\right) .\)
11-19
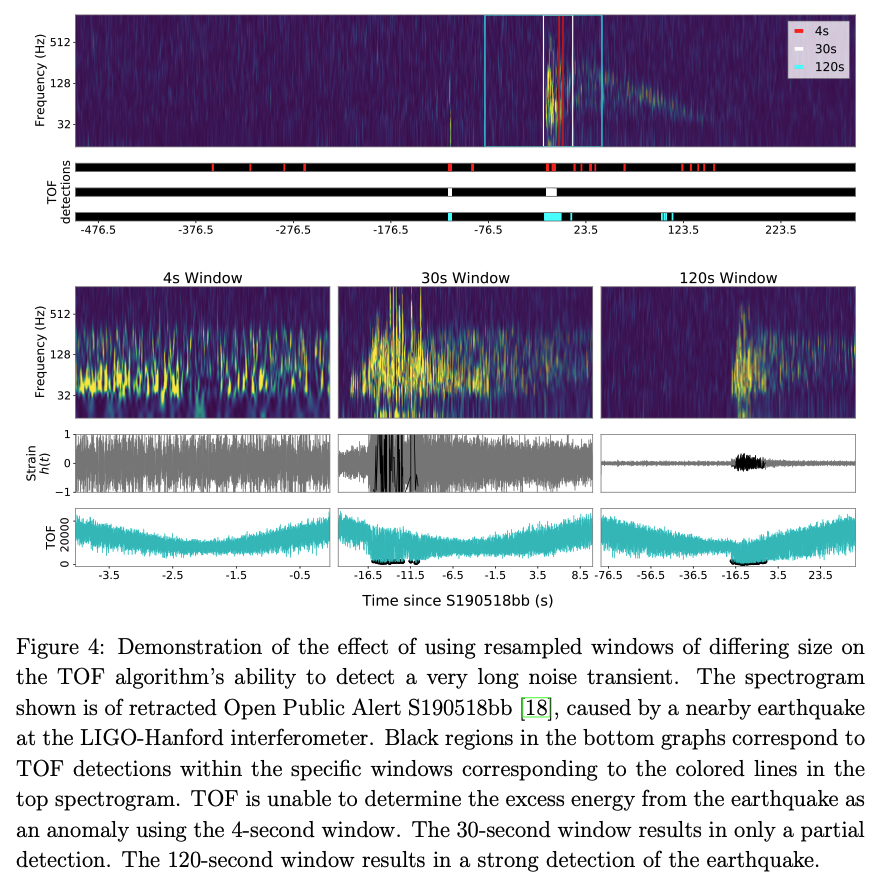
UniMAP: Model-free detection of unclassified noise transients in LIGO-Virgo data using the Temporal Outlier Factor
Propose the Unicorn Multi-window Anomaly-detection Pipeline (UniMAP): a model-free algorithm to identify and characterize transient noise leveraging the Temporal Outlier Factor (TOF) via a multi-window data-resampling scheme. Present the efficacy of this pinepline in detecting glitches.
Temporal Outlier Factor (TOF): the method of algorithmically detecting anomalies in time-series data.
The definition of a time series anomaly provided by TOF is based on two observations:
- Anomalies in time series are \(u n i q u e\)-they are aperiodic, and the data points making up an anomaly tend to be close to each other in time.
- Anomalies in time series are distinct-data trends within an anomaly differ significantly in morphology from the surrounding trends, often in a visually distinct manner.
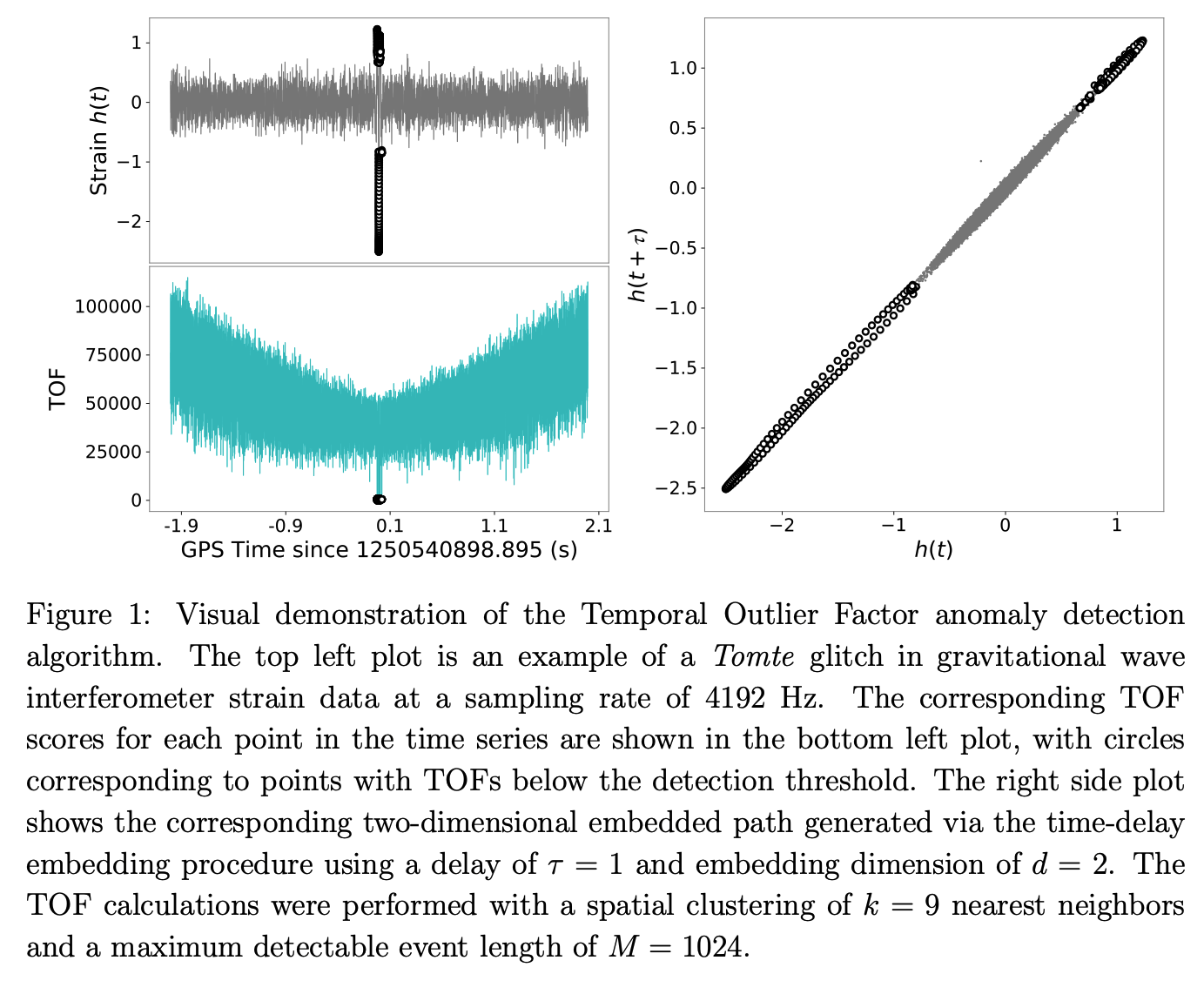
For a unicorn (a data trend with constituent data points close together in time and corresponding spatially clustered points in the time-delay embedded space), the Temporal Outlier Factor of the data point at time \(t\) in a time series \(x\) is therefore defined as \[ \operatorname{TOF}[x, t]=\sqrt{\frac{1}{k} \sum_{i \in k N N}\left(t-t_{i}\right)^{2}} \] where \(k N N\) are the \(k\) nearest neighbors to the data point of interest in the time-delay embedded path \(\mathbf{x}\), and \(t_{i}\) is the corresponding temporal position of each of these \(k\) data points in the original time series.
December
12-3
Wave-optical effects in the microlensing of continuous gravitational waves by star clusters
The continuous GW signals from NS-NS merger events could be persistent for over year-long timescales. At some point during the observational window, if the source comes to lie behind a dense collection of stars, transient gravitational lensing may occur, the lensing would modulate the waveform, induce phase drifts, and ultimately affect parameter inferences concerning the nuclear equation of state and/or magnetic field structure of the neutron star.
Generally speaking, the main challenge in performing legitimately wave-optical calculations is the oscillatory nature of the relevant Fresnel-Kirchhoff diffraction integral (Peters 1974); given a phase profile \(\varphi\), the physical optics calculation involves integrating the exponential \(e^{i \varphi}\) over the aperture, which is infinitely oscillatory owing to Euler's formula. A methodology has recently been developed based on the application of Picard-Lefschetz (PL) theory which is useful in this regard.
As it stands, the Fresnel-Kirchhoff integral contains a non-local Green's function. The end result is that the amplification factor, \(F=\phi / \phi^{(0)}\), can be written as: \[ F\left(\boldsymbol{x}_{s}\right)=\frac{4 G M_{L}}{c^{3}} \frac{f_{\mathrm{GW}}}{i} \int d^{2} \boldsymbol{x} \exp \left[2 \pi i f_{\mathrm{GW}} t_{d}\left(\boldsymbol{x}, \boldsymbol{x}_{s}\right)\right] \] where \(\boldsymbol{x}\) (lens-plane-projected coordinates) and \(\boldsymbol{x}_{s}\) (sourceplane-projected coordinates) are expressed in units of: \[ \xi_{0}=R_{E} \text { and } \eta_{0}=\frac{D_{O S}}{D_{O L}} R_{E}, \]
12-6
Multi-Messenger Constraints on Magnetic Fields in Merging Black Hole-Neutron Star Binaries
May
5-26
Fast Neutrino Flavor Conversions can Help and Hinder Neutrino-Driven Explosions
- People found for the first time through 2D axial symmetric MHD simulation including FFC effects that the FFC of neutrinos can either facilitate or hinder the explosion processes of core-collapse supernovae (CCSN), depending on the mass of the SN progenitors.
- FFC refers to the neutrino-neutrino effects in usually the high neutrino density region, in which happens the so-called bipolar oscillation that significantly enhence the neutrino flavor conversion. Typically, FFC scales are much smaller than the hydrodynamic resolutions.
- Based on their previous 1D work, they use 1D for 2km cores still, but add 80 equidistant lateral grid for the angle discretization. MHD coupled with two-moment scheme of neutrino transports. i.e. applying the lepton conservation condition for the cell.
- 3 different masses and 7 groups of neutrino treatments.