This is a note page in which I have collected my interested arXiv preprints (gr-qc) and ranked in time. All the figures are credited to the corresponding paper linked above them.
Please click here to refresh the page if the formulas are not rendered.
Note: now it's the secon
d year I do my daily readings. The papers I selected and noted here would be more concentrating than the last year :) Some of them maybe my potential supervisor's previous works since I am about to start my PhD this fall.
January
1-21
Spinning Black Holes Fall in Love
- The open question that: whether a black hole can become tidally deformed by an external gravitational field has profound implications for fundamental physics, astrophysics and gravitational-wave astronomy. Love tensors characterize the tidal deformability of compact objects such as astrophysical (Kerr) black holes under an external static tidal field. This work proves that all Love tensors vanish identically for a Kerr black hole in the nonspinning limit or for an axisymmetric tidal perturbation. In contrast to this result, Love tensors are generically nonzero for a spinning black hole.
- Some universal (i.e., equation-of-state independent) I-Love-\(Q\) and I-Love-C relations between the neutron star moment of inertia, quadrupolar tidal Love numbers (TLNs), quadrupole moment and compactness can be used to lift degeneracies among parameters in gravitational-wave signals, enhancing the measurability of the tidal effects.
1-31
Imprints of dark matter on gravitational ringing of supermassive black holes
The authors calculate the complex frequencies of the quasi-normal modes of the supermassive black hole in the dark matter halos. The corresponding gravitational wave spectra with the effects of the dark matter halos and their detectability have also been discussed.
Since previously only the axial-perturbation sector has been investigated, here it shall move to the polar perturbations by using the technique developed recently for constructing master equation of polar-perturbations for spherical symmetric BHs.
There are several halo profile that had been taken into consideration:
- The universal rotation curve (URC) profile has distribution of the form: \[ \rho(r)=\frac{\rho_{0} r_{0}^{3}}{\left(r+r_{0}\right)\left(r^{2}+r_{0}^{2}\right)} \]
February
2-1
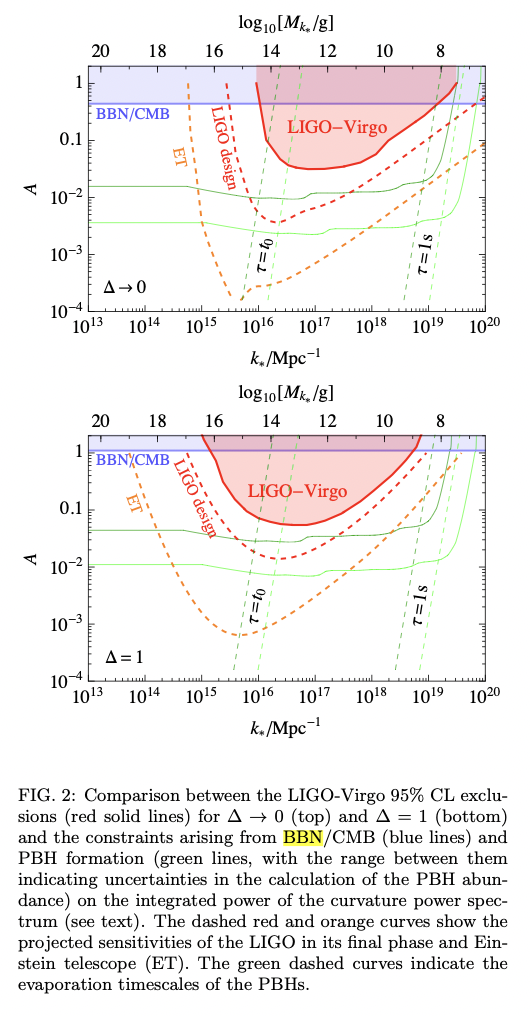
Search for a scalar induced stochastic gravitational wave background in the third LIGO-Virgo observing run
- Perform a Bayesian search of formation of primordial black holes from inflationary fluctuations, which is accompanied by a scalar induced gravitational wave background in the data from Advanced LIGO and Virgo’s first, second and third observing runs. The search shows no evidence for such a background. The LIGO-Virgo bound is stronger than the in- direct bounds on the abundance of GWs arising from big bang nucleosynthesis (BBN).
2-17
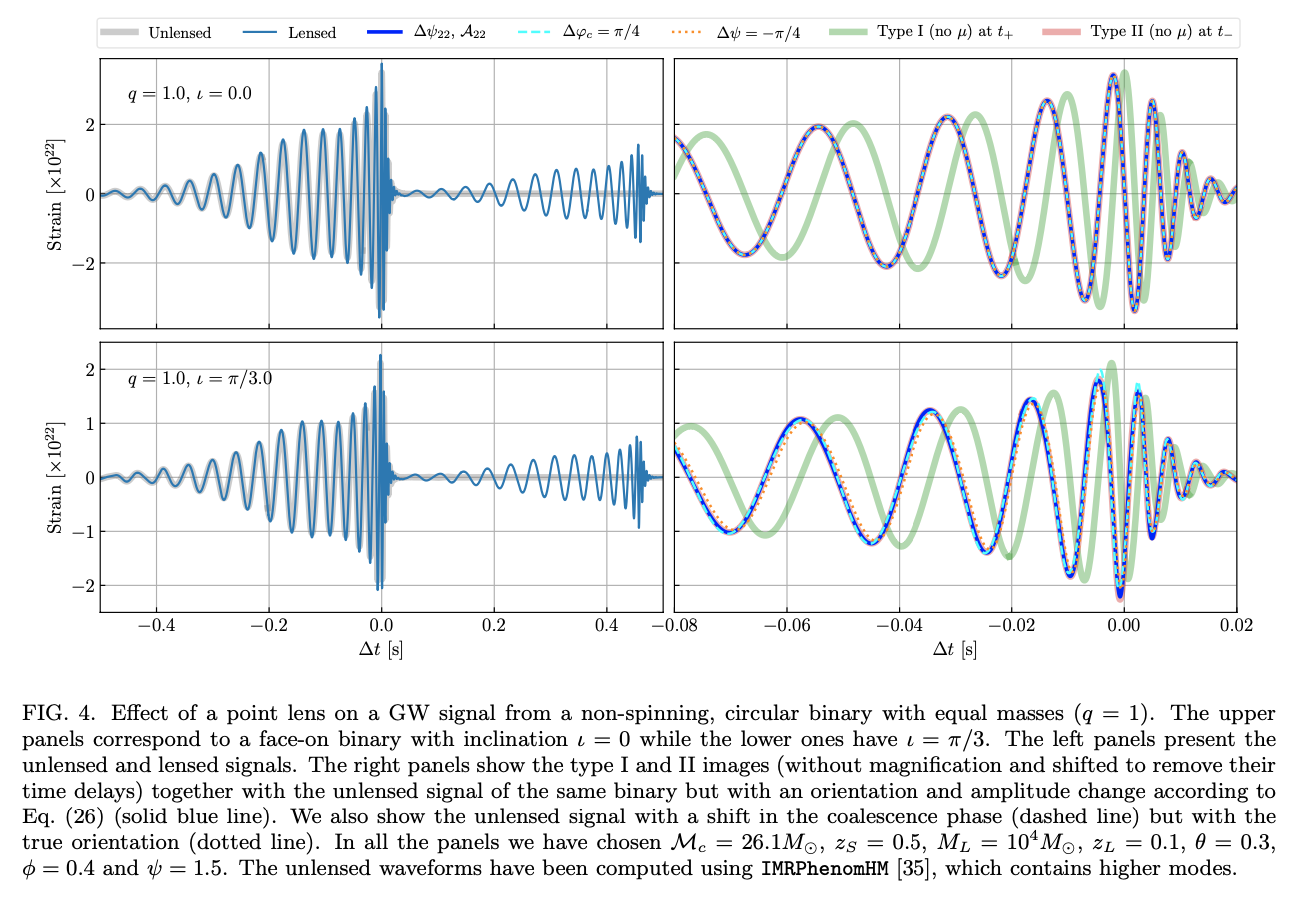
Phase effects from strong gravitational lensing of gravitational waves
The short wavelength lensed GWs (ignoring wave effects) have phase shifts that are typically degenerate with either a shift in the coalescence phase or a detector and inclination dependent shift in the orientation angle. However, the presence of precession or eccentricity and higher harmonic modes would break this degeneracy. An exact template with a phase shift in Fourier space can always be constructed to fit any lensed image. The authors conclude that an optimal strong lensing search strategy would incorporate phase information in all stages of the identification of strong-lensing, with an exact treatment in the final assessment of the probability of multiple lensed events. This work clarifies the role that strong lensing plays in the phase evolution of GWs: how it can lead to apparent deviations from GR, how it can affect the detectability of GW events, and how it can be exploited to help identify cases of strong gravitational lensing of gravitational wave sources.

For a given \(\vec{\theta}\), the time delay between the lensed and unlensed path in the thin lens approximation is determined by: \[ t_{d}\left(\vec{\theta}, \vec{\theta}_{S}\right) \approx \frac{1}{c} \frac{D_{L} D_{S}}{2 D_{L S}}\left|\vec{\theta}-\vec{\theta}_{S}\right|^{2}+t_{\Phi}(\vec{\theta}) \] The first piece is the geometric time delay and \(t_{\Phi}\) is the Shapiro time delay from the time dilation due to traversing a lensed path \(s\) through the gravitational potential \(\Phi\) : \[ t_{\Phi} \approx-\frac{2}{c^{3}} \int \Phi d s \] The resulting lensed wave at the observer position will generically be given by: \[ S_{L}\left(t, \vec{\theta}_{S}\right)=\int \frac{d \omega}{2 \pi} e^{-i \omega t} F\left(\omega, \vec{\theta}_{S}\right) S_{\omega} \] where we have ignored the polarization of the wave, which changes negligibly due to lensing (see Appendix A). Here, \(S_{\omega}=\int d t e^{i \omega t} S(t)\) is the Fourier transform of the unlensed wave source \(S(t)\), with time referenced to the detection epoch. The amplification factor: \[ F\left(\omega, \vec{\theta}_{s}\right)=\frac{D_{L} D_{S}}{D_{L S}} \frac{1}{c} \frac{\omega}{2 \pi i} \int d^{2} \theta e^{i \omega t_{d}\left(\vec{\theta}_{,} \vec{\theta}_{S}\right)} \] which multiplies the wave in Fourier space, takes into account all possible paths arriving to the observer.
In the case of a thin lens, the light bundles associated with the observed images can pass through at most two caustics. If there are no caustics, the image corresponds to a local minimum of \(t_{d}\) and is said to be of type I. If there is one caustic, it corresponds to a saddle point of \(t_{d}\) and is said to be of type II. If there are two caustics, it corresponds to a local maximum of \(t_{d}\) and is said to be of type III.
2-21
Detecting fundamental fields with LISA observations of gravitational waves from extreme mass-ratio inspirals
The Laser Interferometer Space Antenna, LISA, will detect gravitational wave signals from extreme mass-ratio inspirals, where a stellar mass compact object orbits a supermassive black hole and eventually plunges into it. This paper reports on LISA's capability to detect whether the smaller compact object in an extreme mass-ratio inspiral is endowed with a scalar field, and to measure its scalar charge-a dimensionless quantity that acts as a measure of how much scalar field the object carries. By direct comparison of signals, the authors show that LISA will be able to detect and measure the scalar charge with an accuracy of the order of per cent, which is an unprecedented level of precision. This result is independent unprecedented level of precision. This result is independent of the origin of the scalar field and of the structure and other properties of the small compact object, so it can be seen as fundamental fields.
An EMRI in which the secondary object (which can be a neutron star, a black hole or something more exotic) moves in the spacetime generated by the primary body and is endowed with a massless scalar field configuration, in a local reference frame \(\left\{\tilde{x}^{\mu}\right\}\) centred on the secondary body, has the scalar field with the form: \[ \varphi=\varphi_{0}+\frac{\mu d}{\tilde{r}}+\mathcal{O}\left(\frac{\mu^{2}}{\tilde{r}^{2}}\right) \] where \(\tilde{r}\) is the radial coordinate, \(\mu \ll M\) is the mass of the secondary body, \(d\) is its dimensionless scalar charge, \(\varphi_{0}\) is the asymptotic value of the scalar field, and it's using geometric units \(G=c=1\), with \(G\) and \(c\) being the gravitational constant and the speed of light, respectively.
The orbital energy of the particle decreases due to the total energy emission: \[ \dot{E}_{\text {orb }}=-\dot{E}_{\text {grav }}-\dot{E}_{\text {scal }}, \] where \(\dot{E}_{\text {grav }}\) is the gravitational flux. The scalar flux affects the orbital evolution of the secondary body. Since the \(G W\) phase is determined by the orbital evolution, the scalar-field emission contributes to the GW phase of the EMRI.
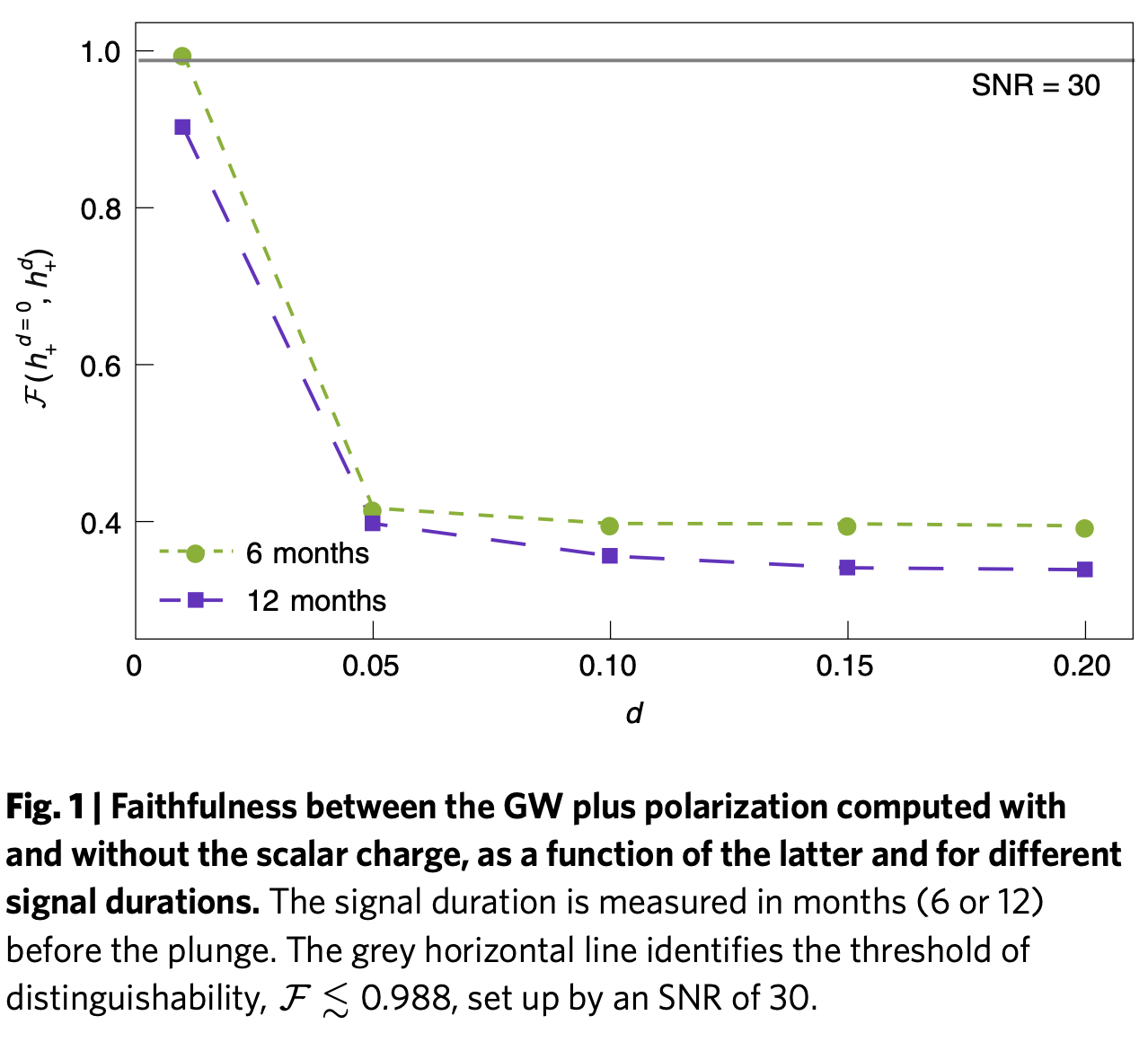
2-28
On the detection of a cosmic dawn signal in the radio background
The sky-averaged redshifted 21 cm absorption line of neutral hydrogen is a probe of the cosmic dawn - when star formation commenced in the first collapsed objects, is predicted to be revealed by spectral and spatial signatures in the cosmic radio background at long wavelengths. The line profile is determined by the evolving thermal state of the gas, radiation background, Lyman α radiation from stars scattering off cold primordial gas, and relative populations of the hyperfine spin levels in neutral hydrogen atoms. The paper reports a radiometer measurement of the spectrum of the radio sky in the 55–85 MHz band, which shows that the profile found by Bowman et al could be bore out and suggests that the profile found by Bowman et al. is not evidence for new astrophysics or non-standard cosmology.
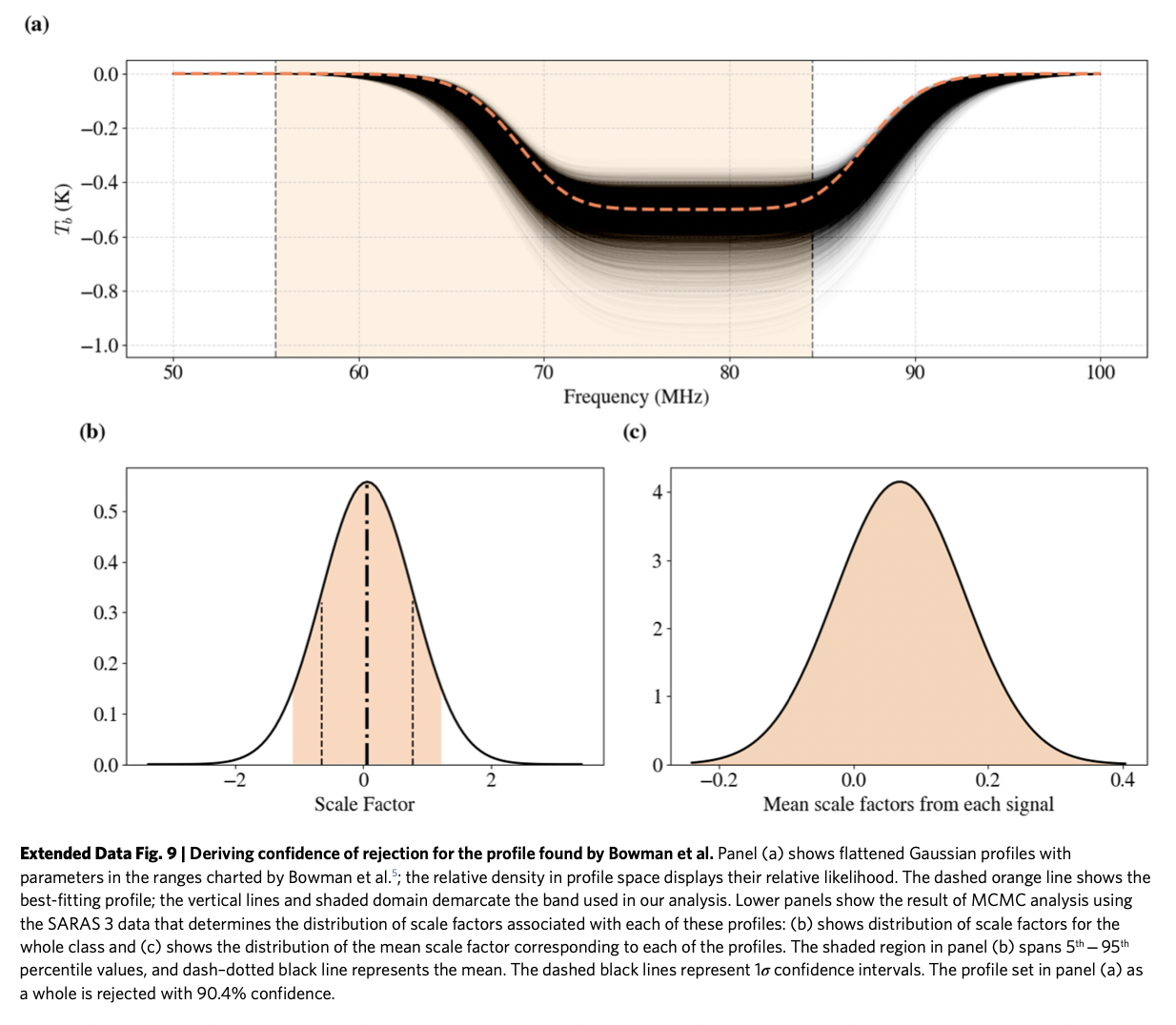
"We have used this distribution of profile parameters and generated a substantially larger number of MCMC walkers by allowing for an additional scale factor parameter for each of their profiles. We then evolved the walkers for each profile, using a sixth-order polynomial to represent the foreground and calibration systematics in this sky spectrum, to model the SARAS 3 spectrum. The analysis for each walker thus followed the same method as described in the main text for the best-fitting profile of Bowman et al. \(^{5}\). The scale factor distributions from our suite of walkers, considering all of the walkers for all of the profiles together, are naturally weighted by the likelihood distribution defined by the data from the EDGES instrument, and constrained by the data from SARAS 3. The scale factors from all walkers, combined to form a single distribution, have the distribution shown in Extended Data Fig. 9b. The mean scale factor is \(0.07\) and the profile set found by Bowman et al. \(^{5}\) as a whole is rejected with \(90.4 \%\) confidence. In Extended Data Fig. \(9 c\) we display the distribution of most-likely scale factors corresponding to each of the profiles in Extended Data Fig. 9a, showing that the scale factor is not consistent with unity for any of the profiles, and is therefore disfavoured by the SARAS 3 data. In Extended Data Fig. 10 we show the distribution of rejection confidence in the profile parameter space."
March
3-1
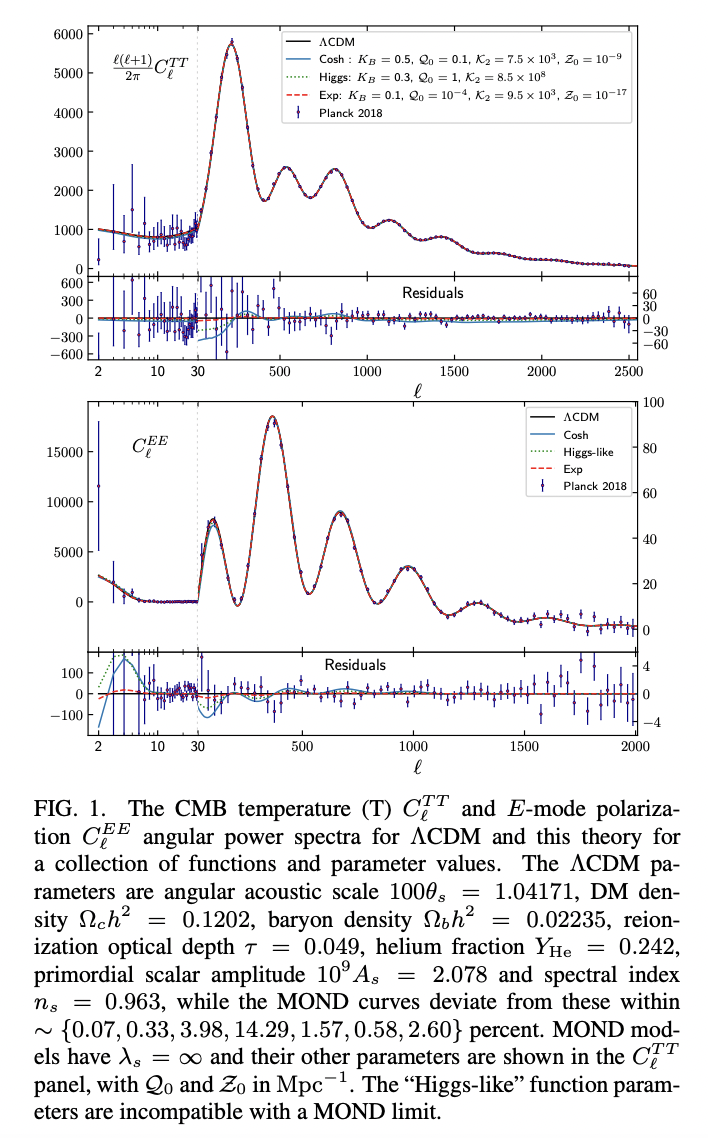
New Relativistic Theory for Modified Newtonian Dynamics
Propose a relativistic gravitational theory leading to modified Newtonian dynamics (MOND). Test it with the observed cosmic microwave background and matter power spectra on linear cosmological scales.
What are the necessary phenomenological facts that any successful MOND theory should lead to? It must (i) return to GR (hence, Newtonian gravity) when \(\vec{\nabla} \Phi \gg a_{0}\) in quasistatic situations while (ii) reproducing the MOND law (1) when \(\vec{\nabla} \Phi \ll a_{0}\). It should also (iii) be in harmony with cosmological observations including the CMB and MPS, (iv) reproduce the observed gravitational lensing of isolated objects without DM halos, and (v) propagate tensor mode gravitational waves (GWs) at the speed of light.
\[ \begin{aligned} S=& \int d^{4} x \frac{\sqrt{-g}}{16 \pi \tilde{G}}\left[R-\frac{K_{B}}{2} F^{\mu \nu} F_{\mu \nu}+2\left(2-K_{B}\right) J^{\mu} \nabla_{\mu} \phi\right.\\ &\left.-\left(2-K_{B}\right) \mathcal{Y}-\mathcal{F}(\mathcal{Y}, \mathcal{Q})-\lambda\left(A^{\mu} A_{\mu}+1\right)\right]+S_{m}[g] \end{aligned} \]
where \(F_{\mu \nu}=2 \nabla_{[\mu} A_{\nu]}, J_{\mu}=A^{\alpha} \nabla_{\alpha} A_{\mu}\), and the Lagrange multiplier \(\lambda\) imposes the unit-timelike constraint on \(A_{\mu}\). In addition \(\mathcal{F}(\mathcal{Y}, \mathcal{Q})\) is a free function of \(\mathcal{Q}=A^{\mu} \nabla_{\mu} \phi\) and \(\mathcal{Y}=\) \(q^{\mu \nu} \nabla_{\mu} \phi \nabla_{\nu} \phi\) where \(q_{\mu \nu}=g_{\mu \nu}+A_{\mu} A_{\nu}\) is the three-metric orthogonal to \(A^{\mu}\). Notice that the above expression is shift symmetric under \(\phi \rightarrow \phi+\phi_{0}\).
3-5
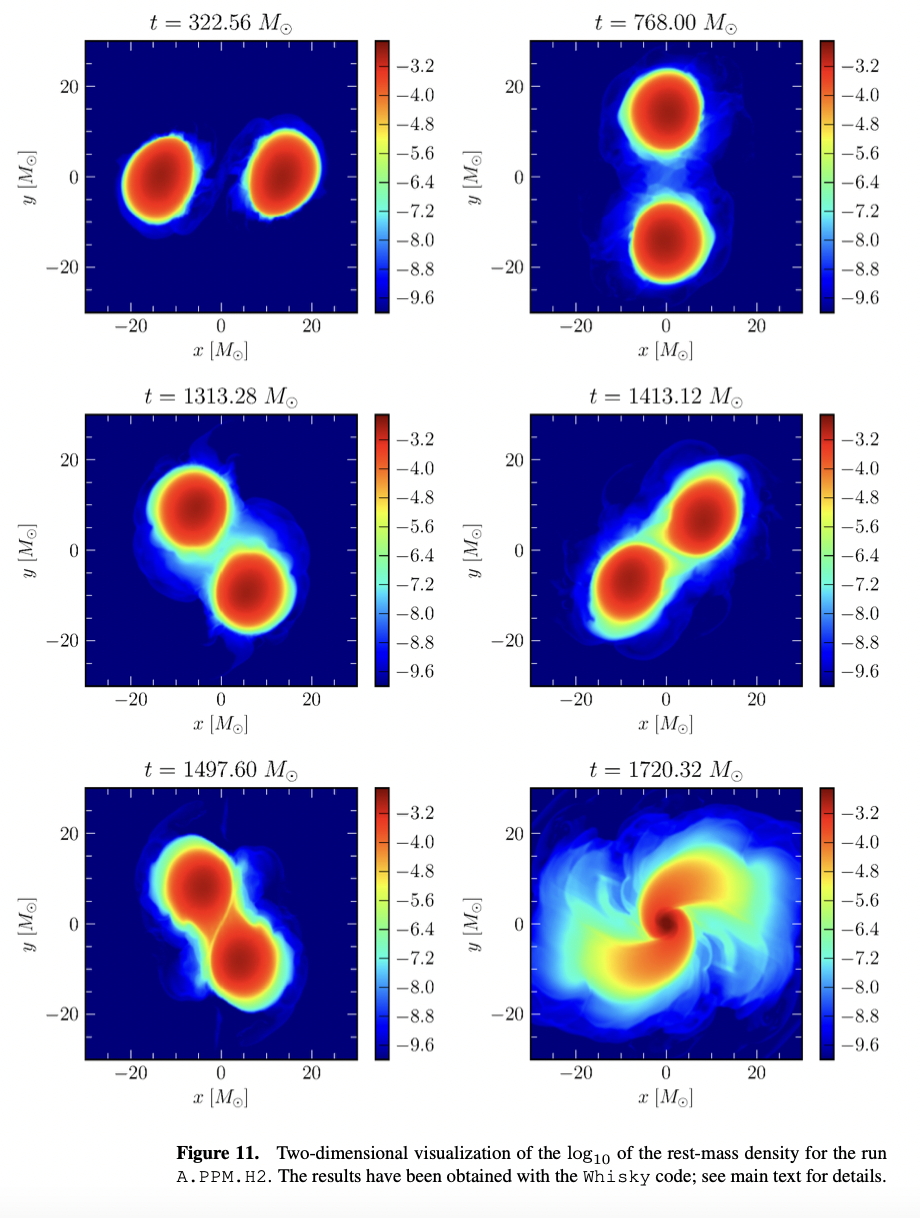
High-Order Fully General-Relativistic Hydrodynamics: new Approaches and Tests
This paper presents a new approach for achieving high-order convergence in fully general-relativistic hydrodynamic simulations. The approach is implemented in WhiskyTHC, a new code that makes use of state-of-the-art numerical schemes and was key in achieving, for the first time, higher than second-order convergence in the calculation of the gravitational radiation from inspiraling binary neutron star.
For the solution of the Einstein equations we adopt the covariant and conformal formulation of the \(Z 4\) equations (CCZ4). We recall that the \(Z 4\) formulation can be obtained from the covariant Lagrangian \[ \Lambda=g^{\mu \nu}\left(R_{\mu \nu}+2 \nabla_{\mu} Z_{\nu}\right) \sqrt{-g}+\Lambda_{m} \] by means of a Palatini-type variational principle, where \(g\) is the metric determinant. The variational principle yields the field equations \[ R_{\mu \nu}+\nabla_{\mu} Z_{\nu}+\nabla_{\nu} Z_{\mu}=8 \pi\left(T_{\mu \nu}-\frac{1}{2} T g_{\mu \nu}\right) \] as well as a set of constraints fixing the connection \[ \nabla_{\mu} g^{\mu \nu}=0 \] and the algebraic constraint \[ Z_{\mu}=0 \text {. } \] The key idea of the \(\mathrm{Z} 4\) formalism is to develop a set of evolution equations starting from the Lagrangian, without explicitly enforcing, i.e. treating \(Z_{\mu}\) as a new independent variable. The resulting set of equations is then strongly hyperbolic, i.e. free from the zero-speed modes of the original ADM system, and the solution of the Einstein equations is obtained exploiting the fact that the \(\mathrm{Z} 4\) evolution system preserves the constraint, i.e. \(\partial_{t}\left(Z_{\mu}\right)=0\). In particular, if the initial-data is constraint satisfying, the \(\mathrm{Z} 4\) evolution recovers the solution of the Einstein equations, even though \(Z_{\mu}\) is an evolved variable. In practice, however, small numerical errors introduce constraint violation during the evolution, for this reason the \(\mathrm{Z} 4\) system is usually modified, with the addition of terms that cancel out in the case in which the constraints are satisfied, to ensure that eventual constraint violations are propagated away and damped exponentially.
The version of \(\mathrm{Z} 4\) is based on a conformal decomposition of the original Z4 system and aims at exploiting well-tested gauge conditions together with the constraint propagation and damping properties of the original Z4 formulation. The CCZ4 system then reads: \[ \begin{aligned} \partial_{t} \tilde{\gamma}_{i j}=-2 \alpha \tilde{A}_{i j}^{\mathrm{TF}}+2 \tilde{\gamma}_{k(i} \partial_{j)} \beta^{k}-\frac{2}{3} \tilde{\gamma}_{i j} \partial_{k} \beta^{k}+\beta^{k} \partial_{k} \tilde{\gamma}_{i j} \\ \partial_{t} \tilde{A}_{i j}=\phi^{2}\left[-\nabla_{i} \nabla_{j} \alpha+\alpha\left(R_{i j}+\nabla_{i} Z_{j}+\nabla_{j} Z_{i}-8 \pi S_{i j}\right)\right]^{\mathrm{TF}}+\alpha \tilde{A}_{i j}(K-2 \Theta)- \\ \partial_{t} \phi=\frac{1}{3} \alpha \phi K-\frac{1}{3} \phi \partial_{k} \beta^{k}+\beta^{k} \partial_{k} \phi \\ \partial_{t} K=-\nabla^{i} \nabla_{i} \alpha+\alpha\left(R+2 \nabla_{i} Z^{i}+K^{2}-2 \Theta K\right)+ \\ \beta^{j} \partial_{j} K-3 \alpha \kappa_{1}\left(1+\kappa_{2}\right) \Theta+4 \pi \alpha(S-3 E) \\ \partial_{t} \Theta=\frac{1}{2} \alpha\left(R+2 \nabla_{i} Z^{i}-\tilde{A}_{i j} \tilde{A}^{i j}+\frac{2}{3} K^{2}-2 \Theta K\right)- \\ Z^{i} \partial_{i} \alpha+\beta^{k} \partial_{k} \Theta-\alpha \kappa_{1}\left(2+\kappa_{2}\right) \Theta-8 \pi \alpha E \\ \partial_{t} \hat{\Gamma}^{i}=2 \alpha\left(\tilde{\Gamma}_{j k}^{i} \tilde{A}^{j k}-3 \tilde{A}^{i j} \frac{\partial_{j} \phi}{\phi}-\frac{2}{3} \tilde{\gamma}^{i j} \partial_{j} K\right)+2 \tilde{\gamma}^{k i}\left(\alpha \partial_{k} \Theta-\Theta \partial_{k} \alpha-\frac{2}{3} \alpha K Z_{k}\right)- \\ 2 \tilde{A}^{i j} \partial_{j} \alpha+\tilde{\gamma}^{k l} \partial_{k} \partial_{l} \beta^{i}+\frac{1}{3} \tilde{\gamma}^{i k} \partial_{k} \partial_{l} \beta^{l}+\frac{2}{3} \tilde{\Gamma}^{i} \partial_{k} \beta^{k}- \\ \tilde{\Gamma}^{k} \partial_{k} \beta^{i}+2 \kappa_{3}\left(\frac{2}{3} \tilde{\gamma}^{i j} Z_{j} \partial_{k} \beta^{k}-\tilde{\gamma}^{j k} Z_{j} \partial_{k} \beta^{i}\right)+ \\ \beta^{k} \partial_{k} \hat{\Gamma}^{i}-2 \alpha \kappa_{1} \tilde{\gamma}^{i j} Z_{j}-16 \pi \alpha \tilde{\gamma}^{i j} S_{j} \end{aligned} \] where \(\Theta \equiv n_{\mu} Z^{\mu}=\alpha Z^{0}, S=\gamma^{i j} S_{i j}, \tilde{\gamma}_{i j}=\phi^{2} \gamma_{i j}\) is the conformal metric with unit determinant \(\phi=\left(\operatorname{det}\left(\gamma_{i j}\right)\right)^{-1 / 6}\), while the extrinsic curvature \(K_{i j}\) is split into its trace \(K \equiv K_{i j} \gamma^{i j}\) and its trace-free components \[ \tilde{A}_{i j}=\phi^{2}\left(K_{i j}-\frac{1}{3} K \gamma_{i j}\right) . \] The three-dimensional Ricci tensor \(R_{i j}\) is split into a part containing conformal terms \(\tilde{R}_{i j}^{\phi}\) and another one containing space derivatives of the conformal metric \(\tilde{R}_{i j}\), defined as \[ \begin{aligned} \tilde{R}_{i j} &=-\frac{1}{2} \tilde{\gamma}^{l m} \partial_{l} \partial_{m} \tilde{\gamma}_{i j}+\tilde{\gamma}_{k(i} \partial_{j)} \tilde{\Gamma}^{k}+\tilde{\Gamma}^{k} \tilde{\Gamma}_{(i j) k}+\tilde{\gamma}^{l m}\left[2 \tilde{\Gamma}_{l(i}^{k} \tilde{\Gamma}_{j) k m}+\tilde{\Gamma}_{i m}^{k} \tilde{\Gamma}_{k j l}\right] \\ \tilde{R}_{i j}^{\phi} &=\frac{1}{\phi^{2}}\left[\phi\left(\tilde{\nabla}_{i} \tilde{\nabla}_{j} \phi+\tilde{\gamma}_{i j} \tilde{\nabla}^{l} \tilde{\nabla}_{l} \phi\right)-2 \tilde{\gamma}_{i j} \tilde{\nabla}^{l} \phi \tilde{\nabla}_{l} \phi\right] \end{aligned} \] The authors adopt the constrained approach in order to enforce the constraints of the conformal formulation; in other words we enforce the condition \(\operatorname{det} \tilde{\gamma}_{i j}=1\) and \(\operatorname{tr} \tilde{A}_{i j}=0\). The evolution variable \(Z_{i}\) of the original \(Z 4\) formulation is now included in the \(\hat{\Gamma}^{i}\) variable of the CCZ4 formulation \[ \hat{\Gamma}^{i} \equiv \tilde{\Gamma}^{i}+2 \tilde{\gamma}^{i j} Z_{j} \] where \[ \tilde{\Gamma}^{i} \equiv \tilde{\gamma}^{j k} \tilde{\Gamma}_{j k}^{i}=\tilde{\gamma}^{i j} \tilde{\gamma}^{k l} \partial_{l} \tilde{\gamma}_{j k} \] Finally, \(\kappa_{1}\) and \(\kappa_{2}\) are constants associated with the constraint damping terms and \(\kappa_{3}\) is an extra constant used to select among different variants of the formulation. In this paper the authors take \(\kappa_{2}=0\) and \(\kappa_{3}=1 / 2\) and recall that the CCZ4 formulation is publicly available through the Einstein Toolkit.
Relativistic Hydrodynamics:
Since the authors assume the neutron-star matter to be described as a perfect fluid, the corresponding energy-momentum tensor is given by: \[ T_{\mu \nu}=\rho h u_{\mu} u_{\nu}+p g_{\mu \nu} \] where \(\rho\) is the rest-mass density, \(u^{\mu}\) is the fluid four-velocity, \(p\) is the pressure and \(h=\) \(1+\epsilon+p / \rho\) is the specific enthalpy. The equations of motion for the fluid are the "conservation" of the stress-energy tensor \[ \nabla_{\mu} T^{\mu \nu}=0 \] and the baryon number conservation \[ \nabla_{\mu}\left(\rho u^{\mu}\right)=0 \text {. } \] These two set of equations are closed by an equation of state (EOS) \(p=p(\rho, \epsilon)\), and the authors here assume a simple ideal-fluid (or Gamma-law EOS) \[ p=(\Gamma-1) \rho \epsilon, \] with \(\Gamma=2\) case. In some of the tests the authors also consider the restriction of this EOS to the isentropic case, i.e. the polytropic EOS: \[ p=K \rho^{\Gamma} . \] The equations of motion are solved in conservation form following the Valencia formulation, and written as \[ \frac{\partial \boldsymbol{F}^{0}(\boldsymbol{u})}{\partial t}+\frac{\partial \boldsymbol{F}^{i}(\boldsymbol{u})}{\partial x^{i}}=\boldsymbol{S}(\boldsymbol{u}) \] with a vector of primitive variables \[ \boldsymbol{u} \equiv\left[\rho, v_{i}, \epsilon\right] \] and conservative variables \[ \boldsymbol{F}^{0}(\boldsymbol{u}) \equiv \sqrt{\gamma}\left[D, S_{j}, \tau\right]=\sqrt{\gamma}\left[\rho W, \rho h W^{2} v_{j}, \rho h W^{2}-p-\rho W\right] \] The fluxes are \[ \boldsymbol{F}^{i}(\boldsymbol{u}) \equiv \sqrt{\gamma}\left[D w^{i}, S_{j} w^{i}+\alpha p \delta_{j}^{i}, \tau w^{i}+\alpha p v^{i}\right] \] while the sources functions are given by \[ \boldsymbol{S}(\boldsymbol{u}) \equiv \sqrt{\gamma}\left[0, \frac{\alpha}{2} S^{l m} \partial_{j} \gamma_{l m}+S_{k} \partial_{j} \beta^{k}-E \partial_{j} \alpha, \alpha S^{i j} K_{i j}-S^{i} \partial_{i} \alpha\right] . \text { (25) } \] In the expressions above the fluid three-velocity measured by the normal observer is defined as \[ v^{i} \equiv \frac{u^{i}}{\alpha u^{0}}+\frac{\beta^{i}}{\alpha} \] while the advection velocity relative to the coordinates is \[ w^{i} \equiv \alpha v^{i}-\beta^{i} \] and the Lorentz factor is defined as \(W \equiv \alpha u^{0}=\left(1-v_{i} v^{i}\right)^{-1 / 2}\). Finally, the authors denoted with \(\gamma\) the determinant of the spatial metric and we have used the fact that \(\sqrt{-g} \equiv \alpha \sqrt{\gamma}\).
The authors have demonstrated the accuracy of the code in a series of classical tests involving the linear and nonlinear evolution of isolated neutron stars. In particular, they have shown that their code is able to stably evolve isolated stars for a long time and can attain high order (i.e. third) of convergence in the simulation of the gravitational collapse of nonrotating stars to black holes.
3-6
GW170817: Joint Constraint on the Neutron Star Equation of State from Multimessenger Observations
GW170817 placed an upper bound on certain parameters describing the binary’s tidal interactions. By showing the interpretation of the UV/optical/infrared counterpart of GW170817 with kilonova models with the associated new numerical relativity results, this paper implies a complementary lower bound on the tidal deformability parameter. The joint constraints tentatively rule out both extremely stiff and soft NS equations of state. In this Letter the authors propose and apply to GW170817 a new approach that combines optical/infrared and GW observations, by means of new numerical relativity results, to derive strong joint constraints on the tidal deformability of NSs.
Presently, the strongest con- straint comes from the fact that the maximum mass for NSs must be larger than about \(2 M_{\odot}\) .
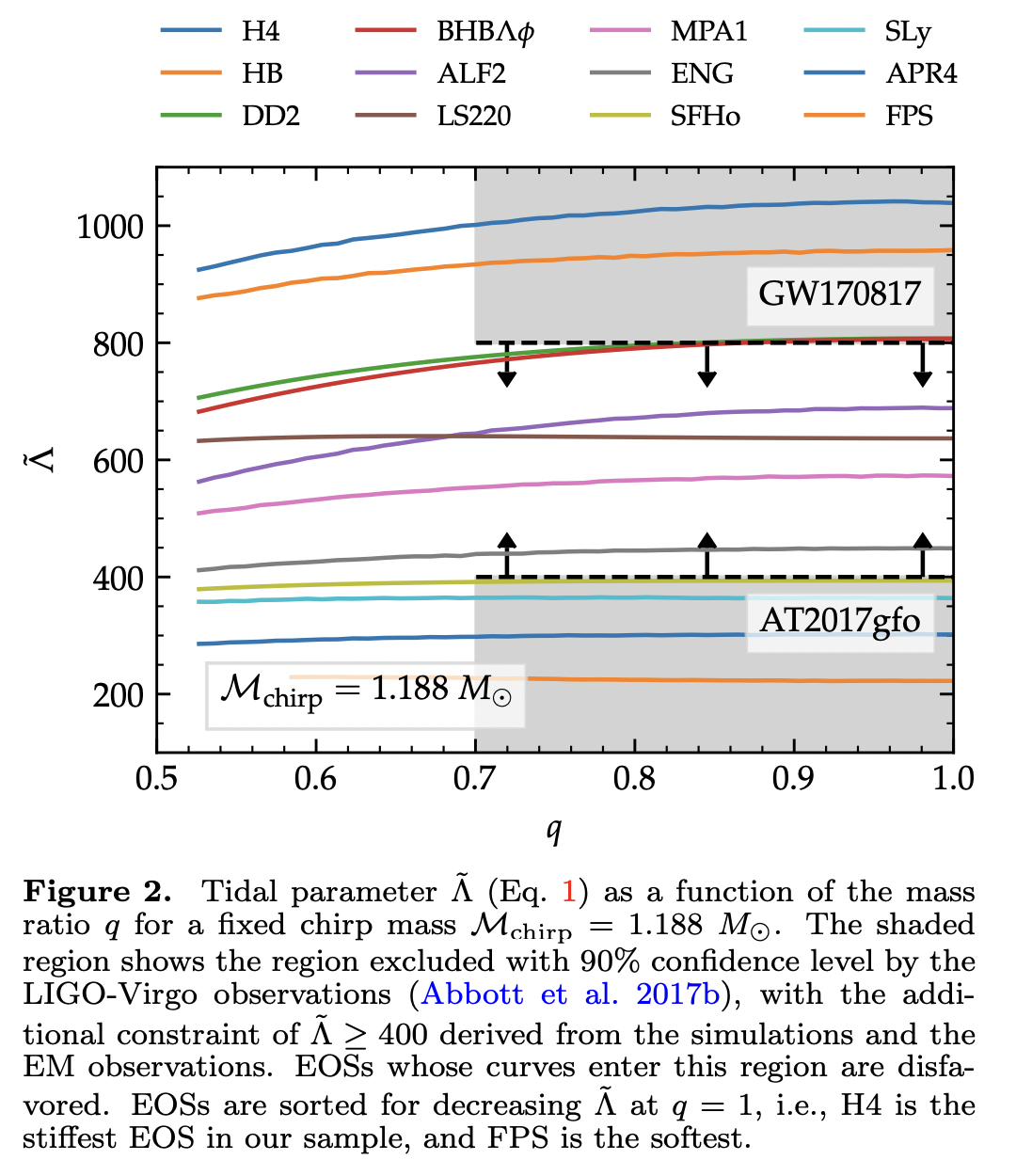
These results show that numerical relativity simulations are key to exploiting the potential of multimessenger observations. While GW data bounds the tidal deformability of NSs from above, the EM data and our simulations bound it from below. The result is a competitive constraint already after the first detection of a merger event. This method is general, it can be applied to future observations and used to inform the priors used in the GW data analysis. The authors anticipate that, with more observations and more precise simulations, the bounds on the tidal deformability of NSs will be further improved.
3-7
THC: a new high-order finite-difference high-resolution shock-capturing code for special-relativistic hydrodynamics
This work presents THC: a new high-order flux-vector-splitting code for Newtonian and special-relativistic hydrodynamics designed for direct numerical simulations of turbulent flows. This work also shows the first systematic comparison of these schemes in Newtonian physics as well as for special-relativistic flows.
Numerical relativistic hydrodynamics has come a long way since the pioneering works by May & White (1966) and Wilson (1972) and it is now playing a central role in modelling of systems involving strong gravity and/or flows with high Lorentz factors. Example of applications are relativistic jets, core-collapse supernovae, merger of compact binaries and the study of gamma-ray bursts [see Mart ́ı & Mu ̈ller (2003) and Font (2008) for a complete overview].
In all of these areas the progress has been continuous over the past few years to the point that relativistic computational fluid dynamics is starting to provide a realistic description of many relativistic-astrophysics scenarios [see, e.g. Rezzolla et al. (2011)]. Key factors in this progress have been the switch to more advanced and accurate numerical schemes, and in particular the adoption of high resolution shock capturing (HRSC) schemes (Martí et al. 1991; Schneider et al. 1993; Banyuls et al. 1997; Donat et al. 1998; Aloy et al. 1999; Baiotti et al. 2003) and the progressive inclusion of more "physics" for a more accurate description of the different scenarios. Examples of the latter are the inclusion of magnetic fields (Koide et al. 1999; Del Zanna et al. 2003; Gammie et al. 2003; Komissarov 2004; Duez et al. 2005; Neilsen et al. 2006; Antón et al. 2006; Giacomazzo & Rezzolla 2007) the use of realistic tabulated equations of state, [see, e.g. Sekiguchi et al. (2011)], and the description of radiative processes (Farris et al. 2008; Sekiguchi 2010; Zanotti et al. 2011).
==The development of more accurate numerical tools for relativistic hydrodynamics is an active and lively field of research. Most of the effort has been directed towards the development of high-order finite-volume (Tchekhovskoy et al. 2007; Duffell & MacFadyen 2011) and finite-difference (Zhang & MacFadyen 2006; Del Zanna et al. 2007) schemes, but many alternative approaches have been also proposed, including finite-element methods (Mann 1985; Meier 1999), spectral methods (Gourgoulhon 1991), smoothedparticle-hydrodynamics (Siegler & Riffert 2000; Rosswog 2010) and discontinuous Galerkin methods (Dumbser & Zanotti 2009; Radice & Rezzolla 2011).==
Finally, THC represents the first step towards the implementation of new and high-order methods for the accurate study of general-relativistic problems, such as the inspiral and merger of binary neutron stars (Baiotti et al. 2011) and their relation with gamma-ray bursts (Rezzolla et al. 2011). In fact, the transition towards higher-order methods is now a necessary and an inevitable step for a more realistic description of the complex phenomenology associated with these relativistic-astrophysics processes.
Multimessenger Parameter Estimation of GW170817
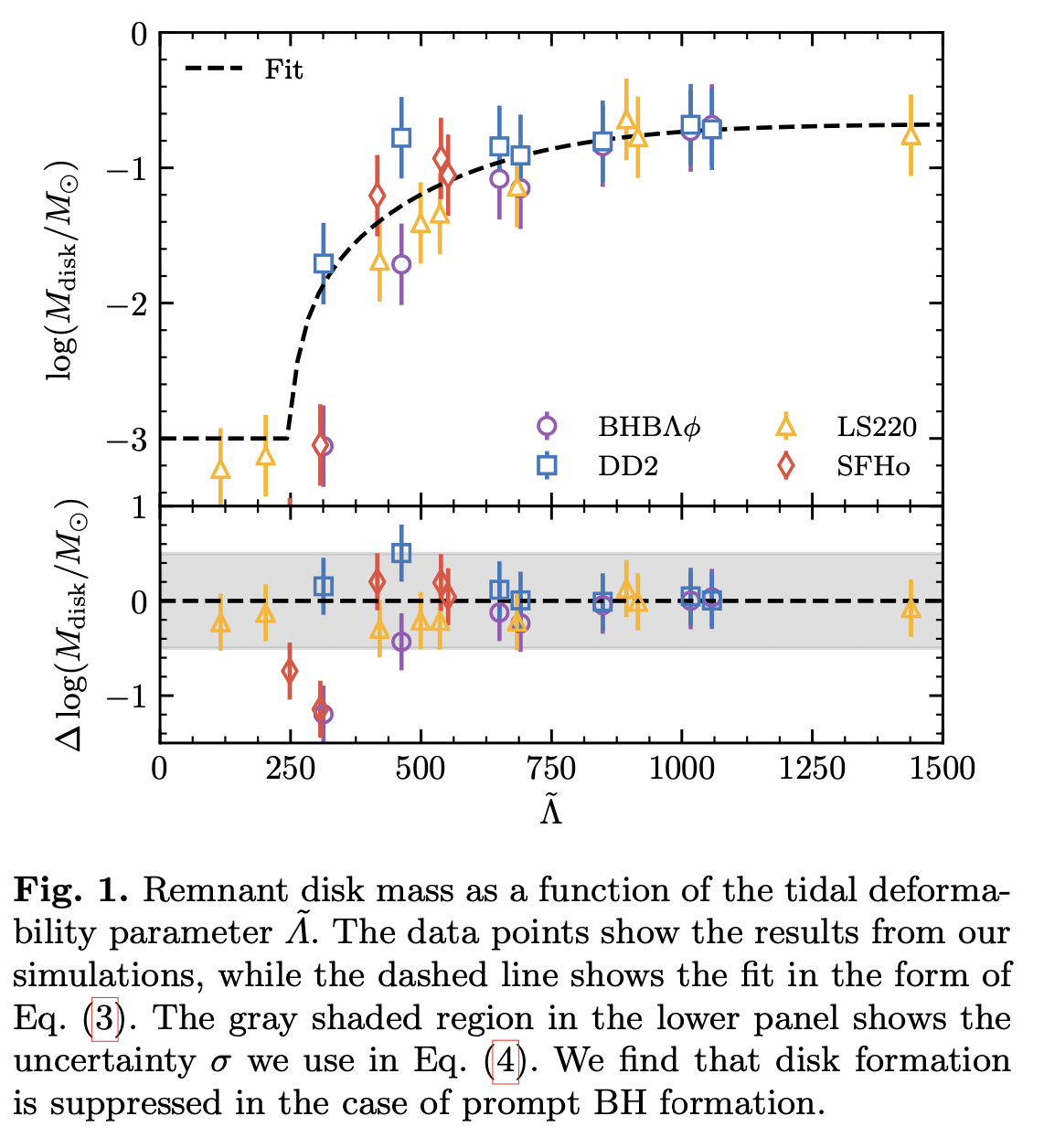
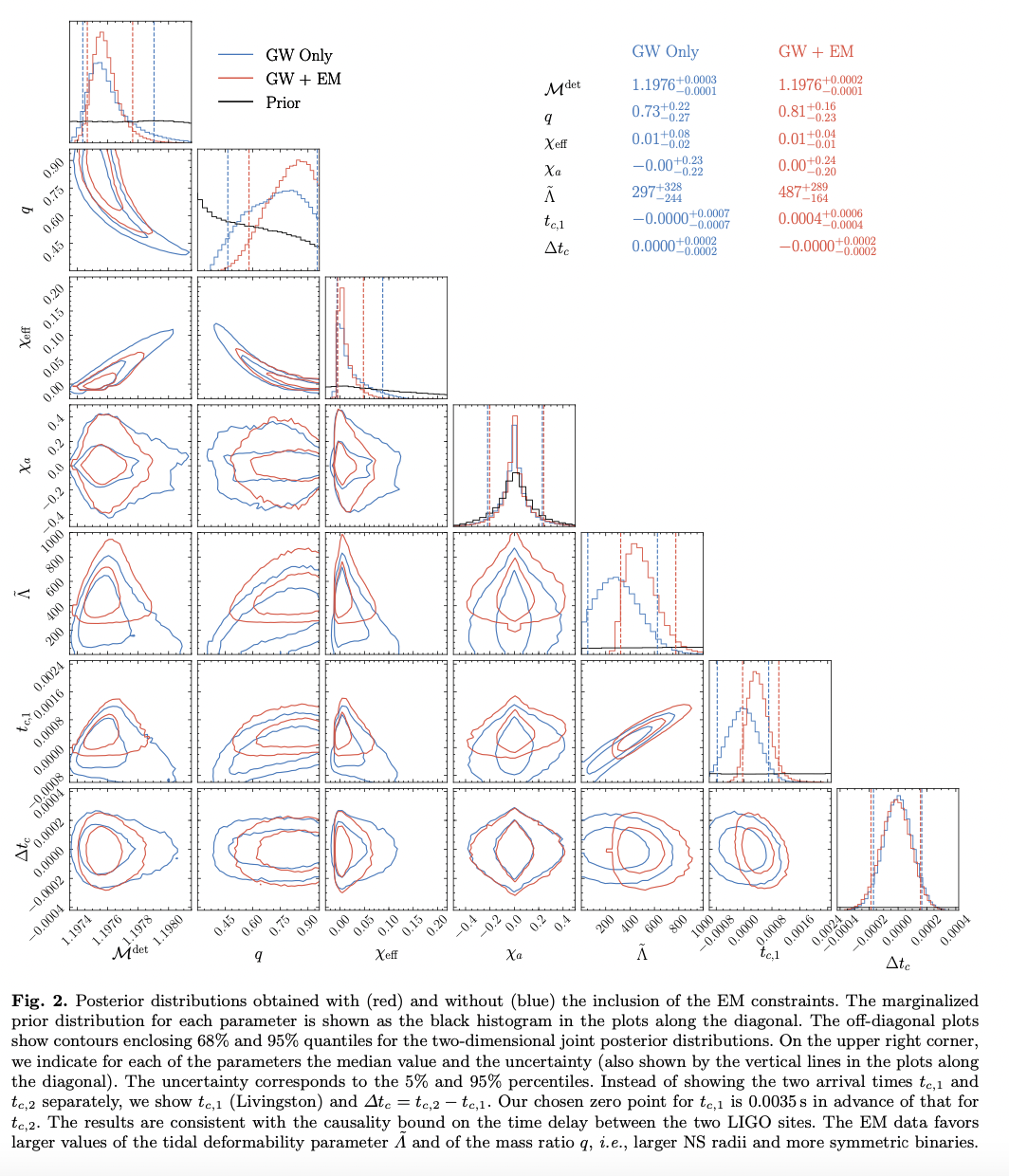
This paper combines gravitational wave \((\mathrm{GW})\) and electromagnetic \((\mathrm{EM})\) data to perform a Bayesian parameter estimation of the binary neutron star (NS) merger GW170817. The EM likelihood is constructed from a fit to a large number of numerical relativity simulations in which a lower bound on the mass of the remnant's accretion disk is inferred from the modeling of the EM light curve. In comparison with previous works, this analysis yields a more precise determination of the tidal deformability of the binary, for which the EM data provide a lower bound, and of the mass ratio of the binary, with the EM data favoring a smaller mass asymmetry.
Assuming \(\mathrm{GW}\) and \(\mathrm{EM}\) data to be independent, we can write the joint \(\mathrm{GW}\) and \(\mathrm{EM}\) likelihood as the product of the separate likelihoods, namely \[ P\left[\left\{d_{\mathrm{GW}}, d_{\mathrm{EM}}\right\} \mid \theta\right]=P\left[d_{\mathrm{GW}} \mid \theta\right] P\left[d_{\mathrm{EM}} \mid \theta\right] \] where \(d_{\mathrm{GW}}\) and \(d_{\mathrm{EM}}\) denote the \(\mathrm{GW}\) and \(\mathrm{EM}\) data, respectively.
This work has performed numerical relativity simulations of merging NS using the WhiskyTHC code. The authors considered 29 binaries, including both equal and unequal mass configurations and 4 temperature and composition dependent nuclear EOSs.
3-10
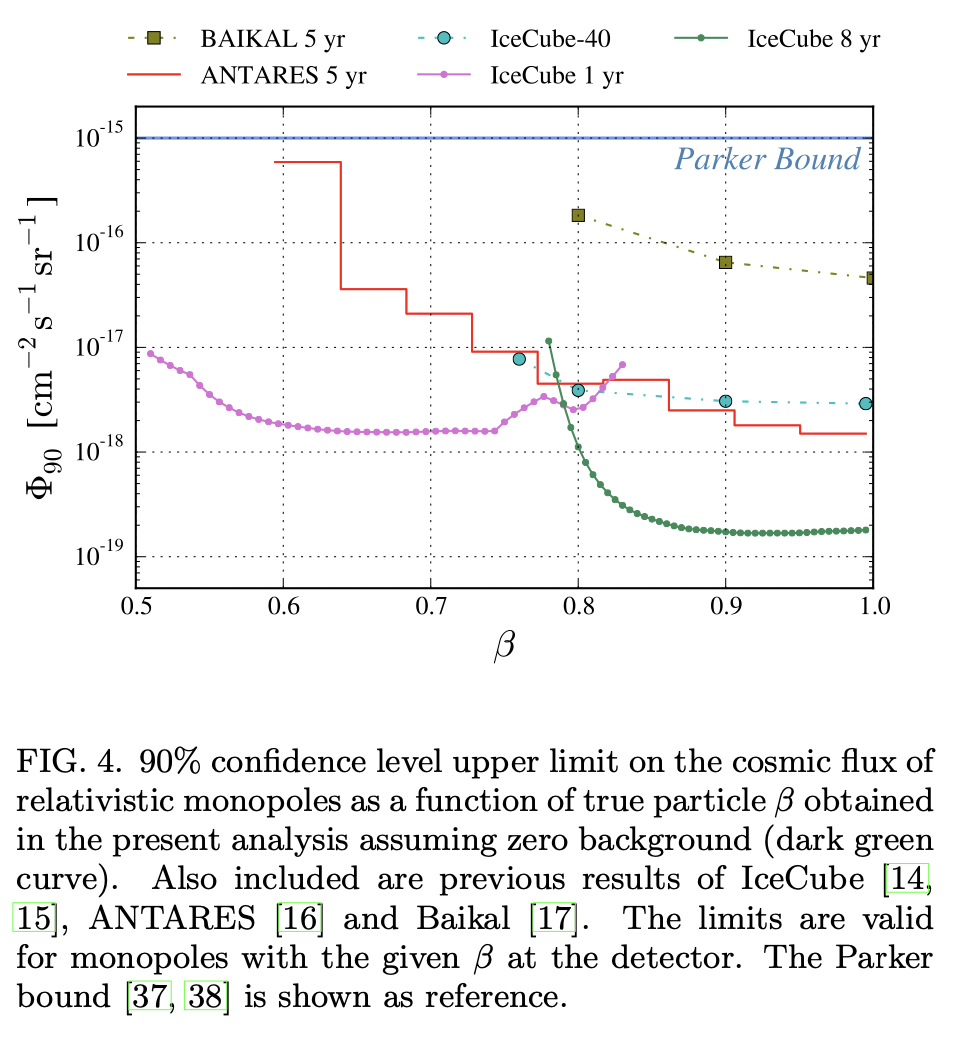
Search for Relativistic Magnetic Monopoles with Eight Years of IceCube Data
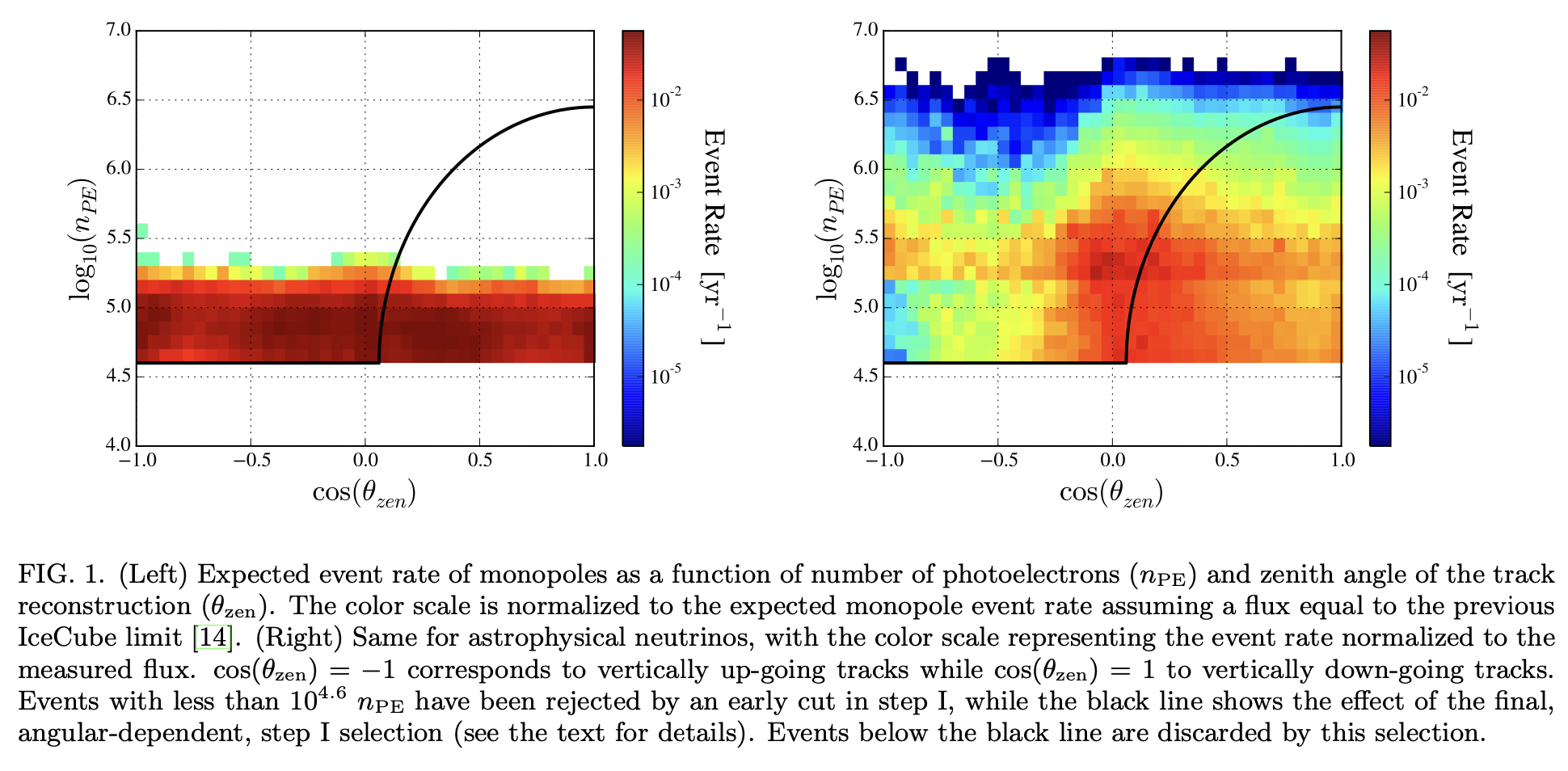
This paper presents an all-sky \(90 \%\) confidence level upper limit on the cosmic flux of relativistic magnetic monopoles using 2886 days of IceCube data. The analysis was optimized for monopole speeds between \(0.750 c\) and \(0.995 c\), without any explicit restriction on the monopole mass. This work constrains the flux of relativistic cosmic magnetic monopoles to a level below \(2.0 \times 10^{-19} \mathrm{~cm}^{-2} \mathrm{~s}^{-1} \mathrm{sr}^{-1}\) over the majority of the targeted speed range. This result constitutes the most strict upper limit to date for magnetic monopoles with \(\beta \gtrsim 0.8\) and up to \(\beta \sim 0.995\) and fills the gap between existing limits on the cosmic flux of nonrelativistic and ultrarelativistic magnetic monopoles.
Magnetic monopoles could have formed in the early Universe as the temperature of the primordial plasma dropped below the energy scale of the GUT symme- try breaking.
Relativistic monopoles (defined as those with \(\beta \geq\) \(0.750\) in what follows) will induce Cherenkov radiation when traversing a dielectric medium faster than the speed of light in the medium, as electrically charged particles do. Therefore Cherenkov detectors can be used to search for cosmic monopoles through the pattern they would leave when passing through the detector.
IceCube is a cubic-kilometer array of digital optical modules (DOMs) deployed in 86 strings at depths between \(1.45\) and \(2.45 \mathrm{~km}\) below the surface of the glacial ice at the South Pole. IceCube uses the ice both as target and detection medium to detect the Cherenkov light from secondary particles produced in neutrino interactions, but it is also sensitive to searches for any new particle that can produce light that is detectable by the optical modules.
3-11
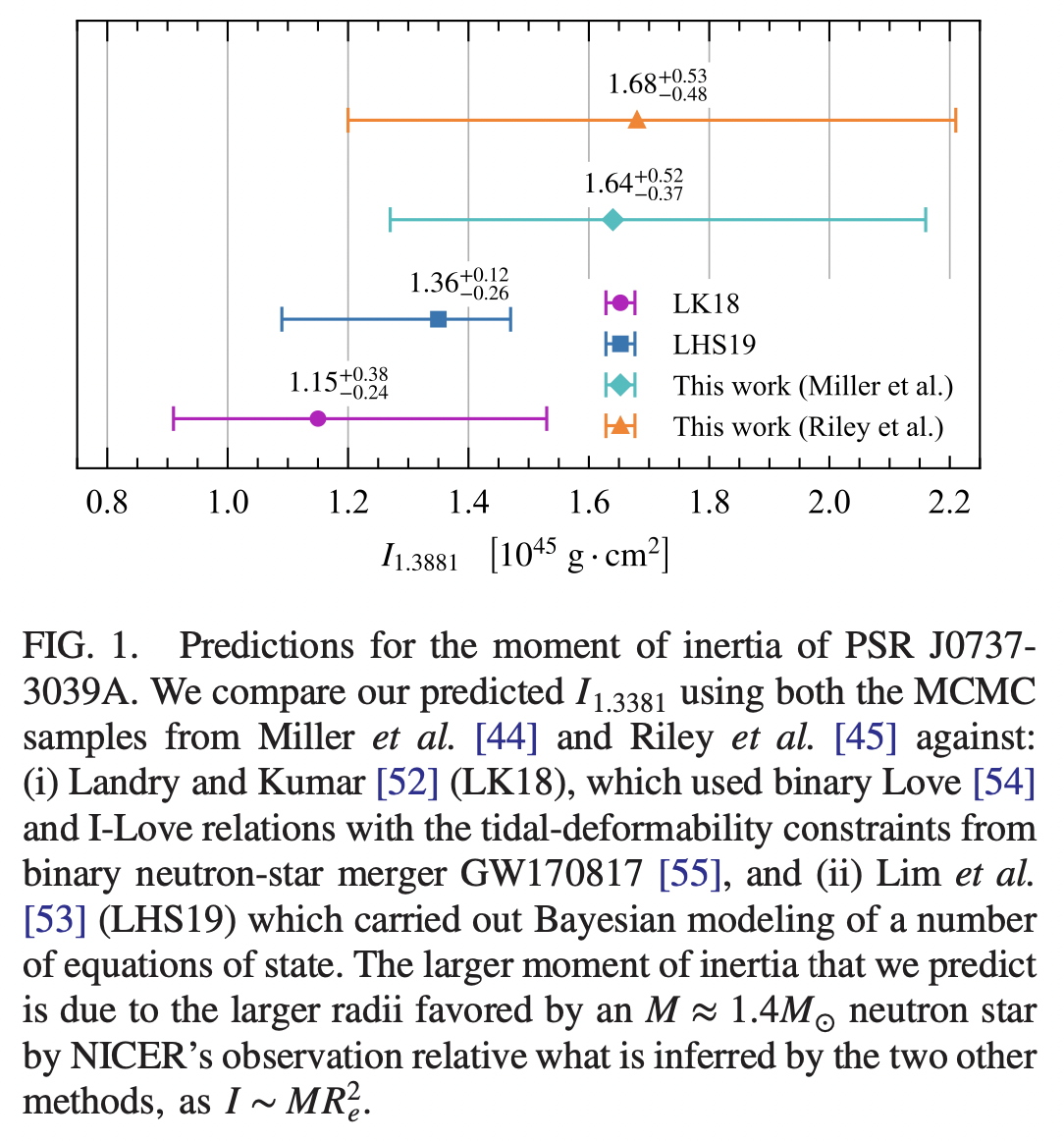
Astrophysical and Theoretical Physics Implications from Multimessenger Neutron Star Observations
The Neutron Star Interior Composition Explorer (NICER) recently measured the mass and equatorial radius of the isolated neutron star PSR J0030+0451. The authors use these measurements to infer the moment of inertia, the quadrupole moment, and the surface eccentricity of an isolated neutron star for the first time. Combining this information with the measurement of the tidal Love number with LIGO/Virgo observations, the authors propose and implement the first theory-agnostic and equation-of-state- insensitive test of general relativity. Specializing these constraints to a particular modified theory, the authors find that consistency with general relativity places the most stringent constraint on gravitational parity violation to date, surpassing all other previously reported bounds by 7 orders of magnitude and opens the path for a future test of general relativity with multimessenger neutron star observations.
When properly nondimensionalized, the moment of inertia \((I)\), the rotational quadrupole moment \((Q)\), and the tidal Love number \((\lambda)\) of neutron stars show a remarkable degree of equation-of-state insensitivity, at a level below \(1 \%[4,5]\). These "I-Love-Q" relations also exist in some modified theories of gravity, although they are different from their general relativity counterparts.
Since carrying out such a test on a theory-by-theory basis would, in general, be complicated, the authors develop and implement a useful parametrization of the I-Love test. From Newtonian gravity, \(\bar{I}\) scales with \(\mathcal{C}^{-2}\), whereas \(\bar{\lambda}\) scales with \(\mathcal{C}^{-5}\). Therefore, \(\bar{I}=C_{\bar{I}} \bar{\lambda} \bar{\lambda}^{2 / 5}\), with \(C_{\bar{I}} \bar{\lambda} \approx 0.52\) a constant that depends on the equation of state very weakly. This calculation can be extended, systematically, in a post-Minkowskian expansion, i.e., an expansion in powers of \(\mathcal{C} \ll 1\). The outcome is that both \(\bar{I}\) and \(\bar{\lambda}\) can be written as a power series in \(\mathcal{C}\) and then be combined (as just described in the Newtonian limit) to obtain \(\bar{I}=\bar{I}(\bar{\lambda})\). The resulting I-Love relation has the same degree of equation-of-state independence as the original I-Love relation. For the neutron star catalog, a parametrization in general relativity of the form \[ \bar{I}_{\mathrm{GR}}=\bar{\lambda}^{2 / 5}\left(c_{0}+c_{1} \bar{\lambda}^{-1 / 5}+c_{2} \bar{\lambda}^{-2 / 5}\right) \] with \(c_{0}=0.584, c_{1}=0.980, c_{2}=2.695\), is sufficient to reproduce our numerical data with mean relative error \(\left\langle\epsilon^{\bar{I}}\right\rangle \leq 2 \times 10^{-3}\). The prefactor \(\bar{\lambda}^{2 / 5}\) is the Newtonian result, while the powers of \(\bar{\lambda}^{-1 / 5}\) inside parenthesis are relativistic (post-Minkowskian) corrections because \(\bar{\lambda}^{-1 / 5} \propto \mathcal{C} \lesssim 0.2\). Given this, we then propose a minimal deformation of the Einsteinian parametrization in above equation of the form \[ \bar{I}_{\mathrm{p}}=\bar{I}_{\mathrm{GR}}+\beta \bar{\lambda}^{-b / 5}, \quad \beta \in \mathbb{R}_{+}, \quad b \in \mathbb{Z}, \] where \(\beta\) and \(b\) are deformation parameters that control the magnitude and type of the deviations from general relativity in the I-Love relation, respectively. Such a parametrization is similar to that successfully used in gravitational-wave tests of general relativity by the LIGO/Virgo Collaboration, the parametrized post-Einsteinian framework.
3-12
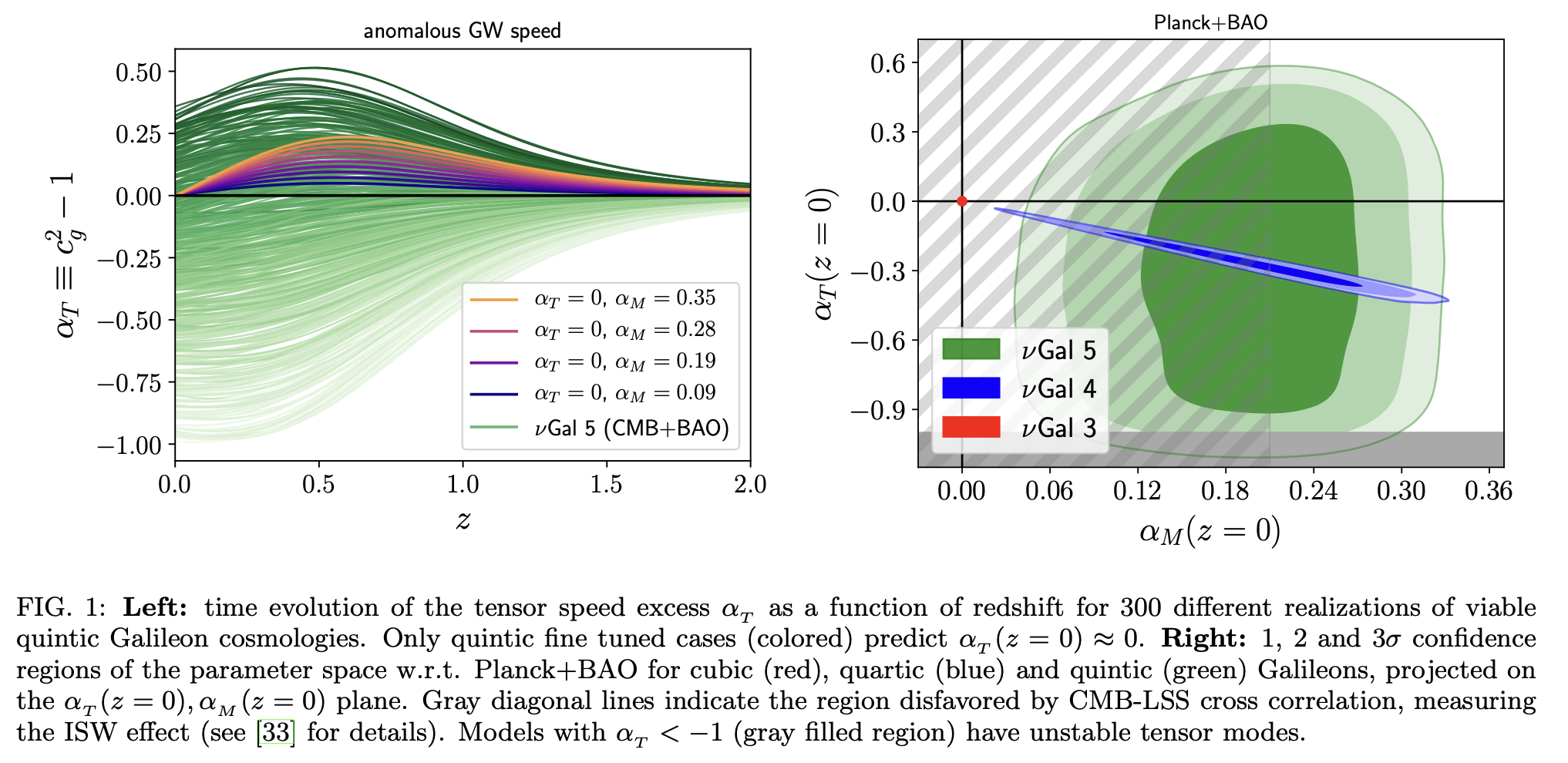
Dark Energy after GW170817: dead ends and the road ahead
Multi-messenger gravitational wave (GW) astronomy has commenced with the detection of the binary neutron star merger GW170817 and its associated electromagnetic counterparts. The almost coincident observation of both signals places an exquisite bound on the \(\mathrm{GW}\) speed \(\left|c_{g} / c-1\right| \leq\) \(5 \cdot 10^{-16}\). The authors use this result to probe the nature of dark energy (DE), showing that a large class of scalar-tensor theories and DE models are highly disfavored. The conclusions could apply to all gravity theory predicting varying \(c_{g}\) such as Einstein-Aether, Hoˇrava gravity, Generalized Proca, TeVeS and other MOND-like gravities.
Each of these events provides complementary information about the BNS merger. The GW signal serves to weight the NS, which are in the range \(0.86-2.26 M_{\odot}\), and to measure the luminosity distance, \(d_{L}=40_{-14}^{+8} \mathrm{Mpc}\). The EM counterparts uniquely identify the host galaxy, NGC4993. Taking the lowest limit \(d_{L}=26 \mathrm{Mpc}\) and a conservative 10s delay between the GW and sGRB the bound on the speed of GWs is: \[ -3 \cdot 10^{-15} \leq c_{g} / c-1 \leq 7 \cdot 10^{-16} . \]
April
4-1
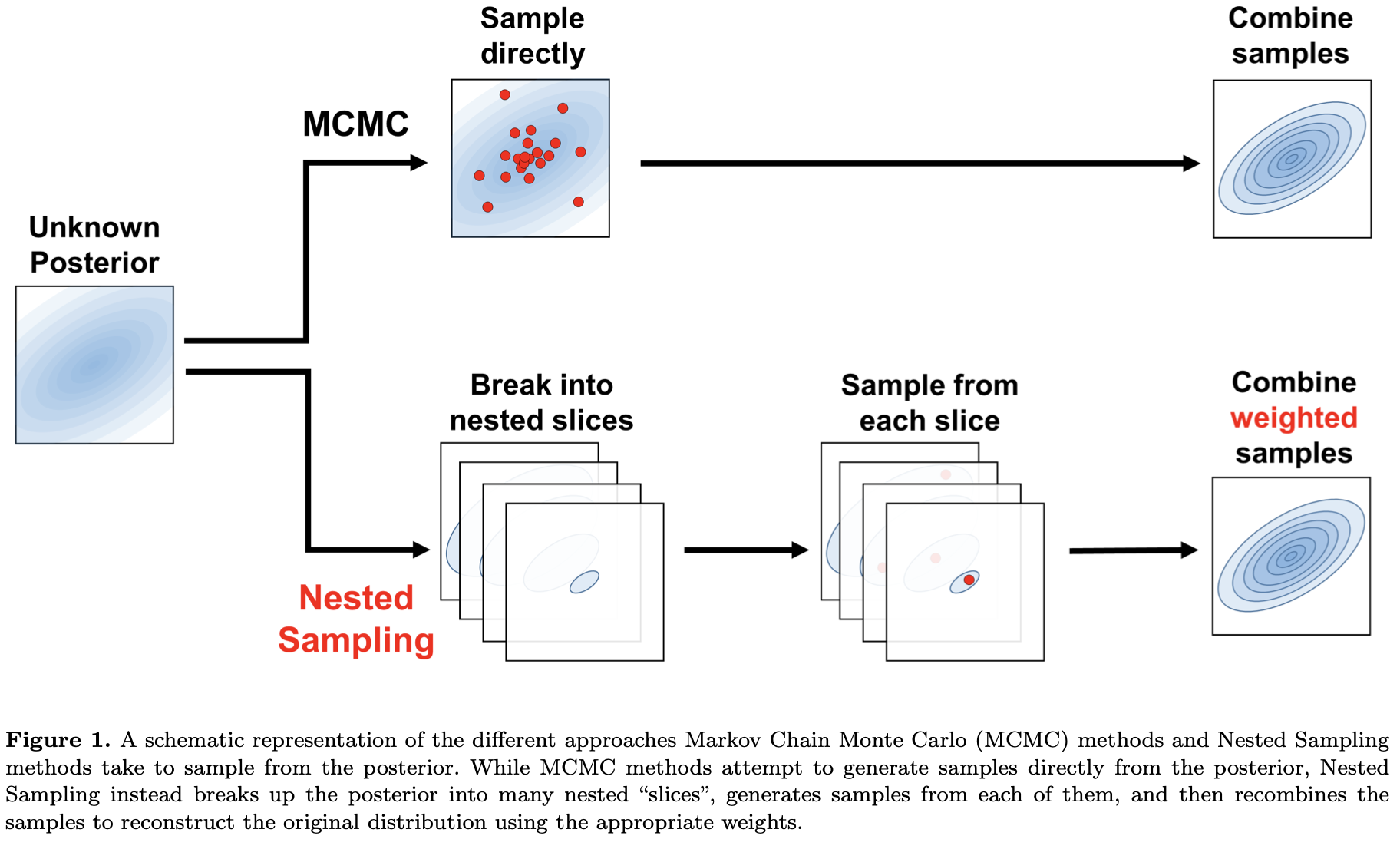
dynesty: A Dynamic Nested Sampling Package for Estimating Bayesian Posteriors and Evidences
- The authors present dynesty, a public, open-source, Python package to estimate Bayesian posteriors and evidences (marginal likelihoods) using Dynamic Nested Sampling. By adaptively allocating samples based on posterior structure, Dynamic Nested Sampling has the benefits of Markov Chain Monte Carlo algorithms that focus exclusively on posterior estimation while retaining Nested Sampling’s ability to estimate evidences and sample from complex, multi-modal distributions. We provide an overview of Nested Sampling, its extension to Dynamic Nested Sampling, the algorithmic challenges involved, and the various approaches taken to solve them. We then examine dynesty’s performance on a variety of toy problems along with several astronomical applications. We find in particular problems dynesty can provide substantial improvements in sampling efficiency compared to popular MCMC approaches in the astronomical literature.
May
5-1
Self-Lensing Flares from Black Hole Binaries: Observing Black Hole Shadows via Light Curve Tomography
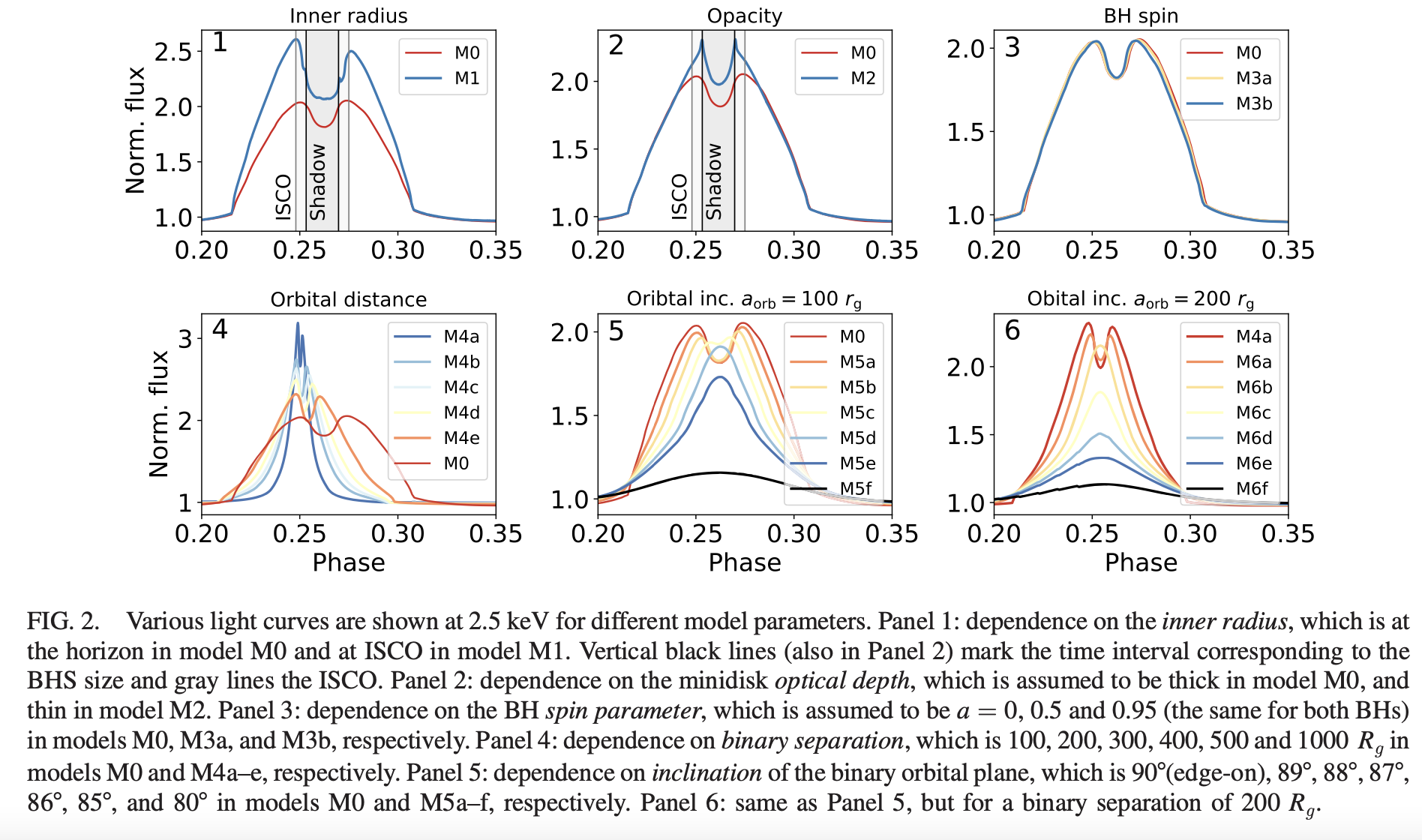
- Supermassive black hole (BH) binaries are thought to produce self-lensing flares (SLFs) when the two BHs are aligned with the line of sight. If the binary orbit is observed nearly edge-on, the relativistic shadow around the background BH can be found. By ray tracing in a binary model, the authors predict that 1% of the current binary candidates could show this feature. This BH tomography method proposed here could make it possible to extract BH shadows that are spatially unresolvable by high-resolution very long base line interferometry (VLBI).
- Supermassive black hole binaries (SMBHBs) are thought to reside in the cores of many galaxies, as a result of galaxy mergers. Their circumbinary disk that transfers material to two minidisks, each orbiting one BH compo- nent. If the viewing angle with respect to the orbital plane is close to edge-on, a minidisk can get lensed by the fore-ground BH resulting in a self-lensing flare (SLF).
5-2
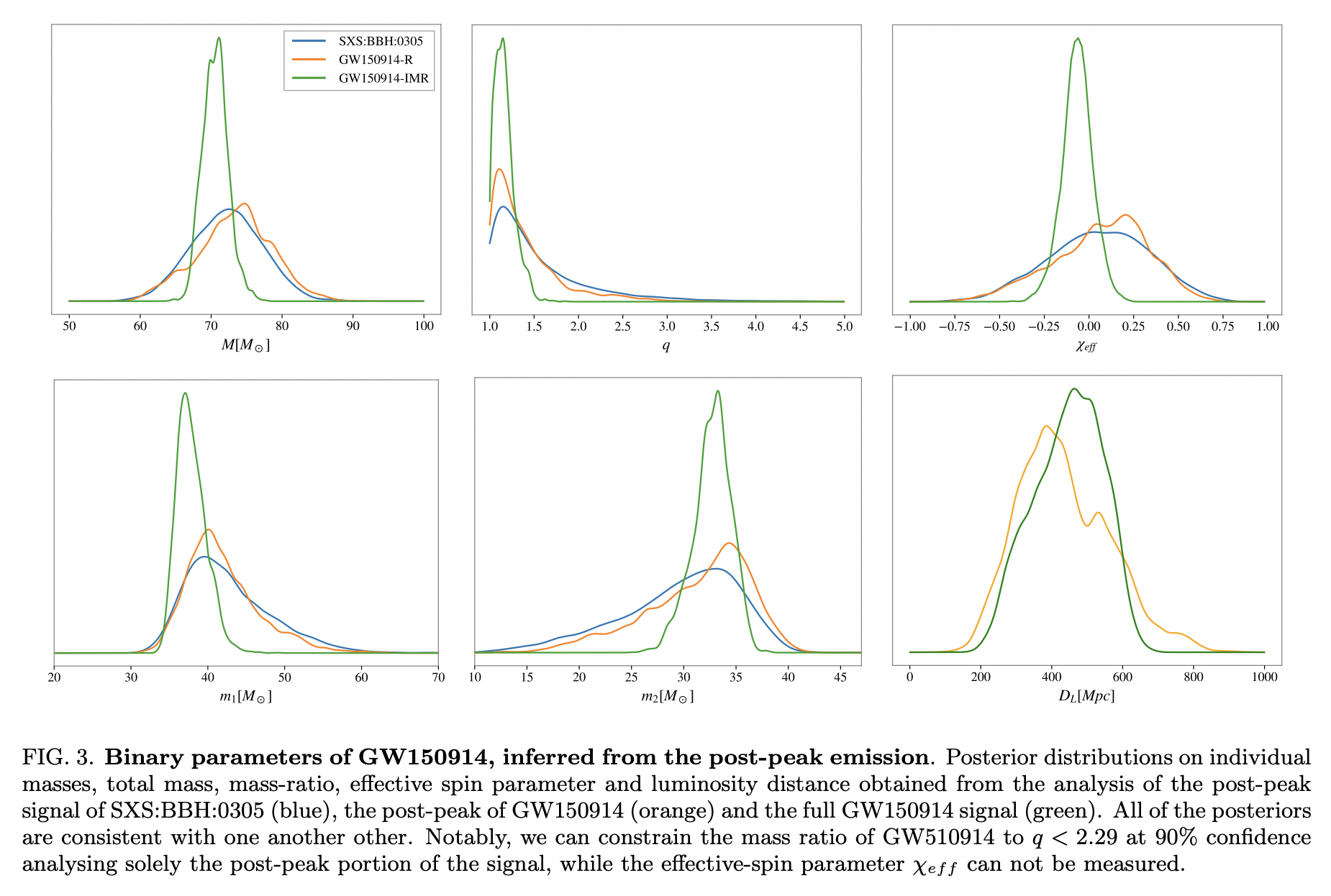
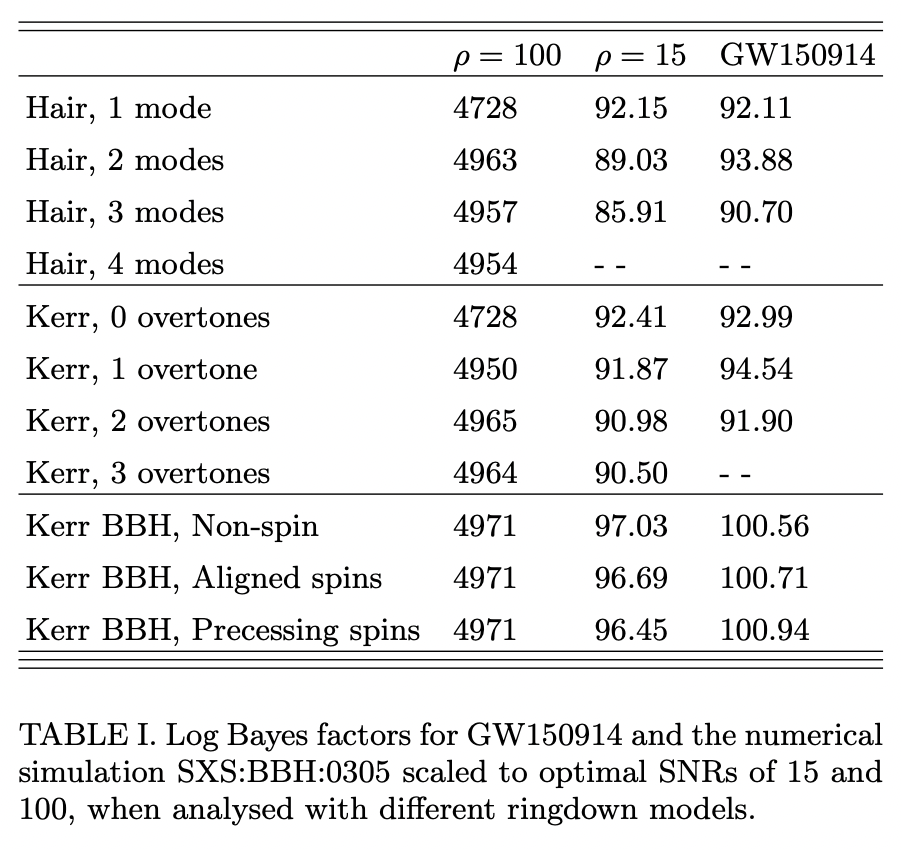
Black-hole spectroscopy, the no-hair theorem and GW150914: Kerr vs. Occam.
Rather than using overtone models, this paper try to use Bayes inference framework parameter estimation with the imposing prior assumptions on the origin of the perturbed black hole that can further constrain the explored parameters: in particular, our knowledge that the ringdown is sourced by a binary black hole merger. Applying this strategy to GW150914 the authors find a natural log Bayes factor of ∼ 6.5 in favour of the Kerr nature of its remnant, indicating that the hairy object hypothesis is disfavoured with < 1 : 600 with respect to the Kerr black-hole one.
Since the post-merger of these waveforms is fitted to full numerical relativity simulations, these naturally include all the overtones, effectively allowing us to place priors on \(\left\{A_{n}, \phi_{n}, f_{n}, \tau_{n}\right\}\) via the binary parameters. In this work, the authors use the phenomenological model for precessing binaries known as IMRPhenomPv2.