Below is my current work's note/draft.
It's a very exciting project!!! Briefly, we just tried to test the possibility to solve einstein equations with finite element method, since it is usually recognized as being more accurate than finite difference methods. Actually, my supervisor had already done the first part of work\(^{[1]}\). And personally, I have really learned a lot of computation skills and MPI running "tricks" only just through this very begining process.
I also found it cool to embed pdf into the webpage. I did this by directly writing html (in which way you may also control its display with several styles, check bootstrap) in markdown and specifying the url path linked to the pdf file.
1 | <object data="https://imqiuyi.com/attaches/GW_FEM_Yi.pdf" type="application/pdf" width="100%" height="800"></object> |
Hope you find it useful too! (Actually, there is an alternative if you are using Hexo developing the website, please check the hexo-pdf plugin.)
Static lensing system
Spining binary black hole lensing system
Motivation:
The propagation properties of continuous gravitational waves (CGWs) are rather simple in its theoretical aspect, while if the CGWs pass through a lensing system, the so-called wave-optics effects would be induced as well as the following modulation of the waveform. It is promising for future space GW detectors (like LISA) to find CGWs, with signal period last for days, weeks, and even months. Hence, some of them will potentially meet the condition that match with the specifc lensing system causing the extreme modulating phenomenon as it propagates through the space and finally accept by us. Therefore, if we understand how the CGWs would be modulated by the lensing system they passed by, we would be able to use them to even extract some information about the lensing system itself, such as the mass-ratio, distance, inspiraling phases of the "scatterer", etc. And most importantly, we would be able to find binary systems even outside the sensitive frequency band of LISA.
Assumptions:
- The source of GWs are BBHs with \(10^5-10^6 M_{sun}\) while the lensing systems are BBHs with \(10^3-10^4 M_{sun}\).
- The wave has no polarization contents.
- The period of the lensing system are quasi-static (period ratio \(\sim\) 100) as well as the frequency of the source GWs.
Current results:
Illustation of our test lensing system.
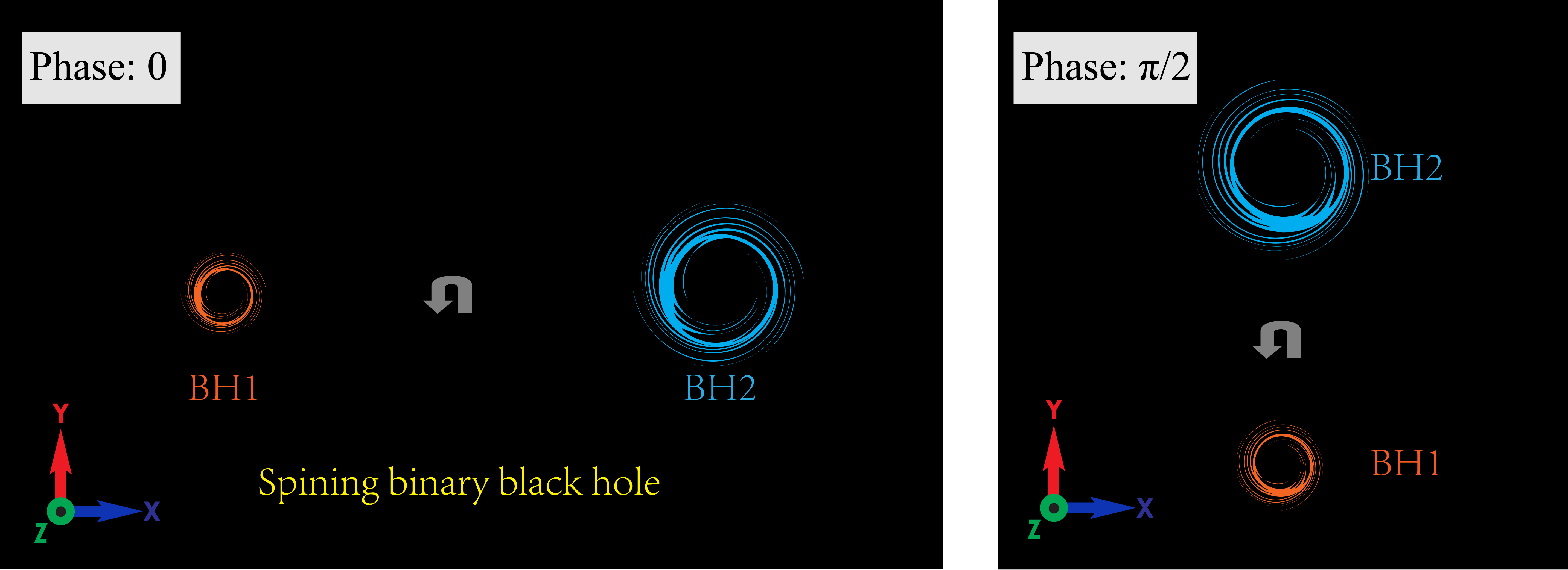
The above figure was created with adobe illustrator 2019 by me.
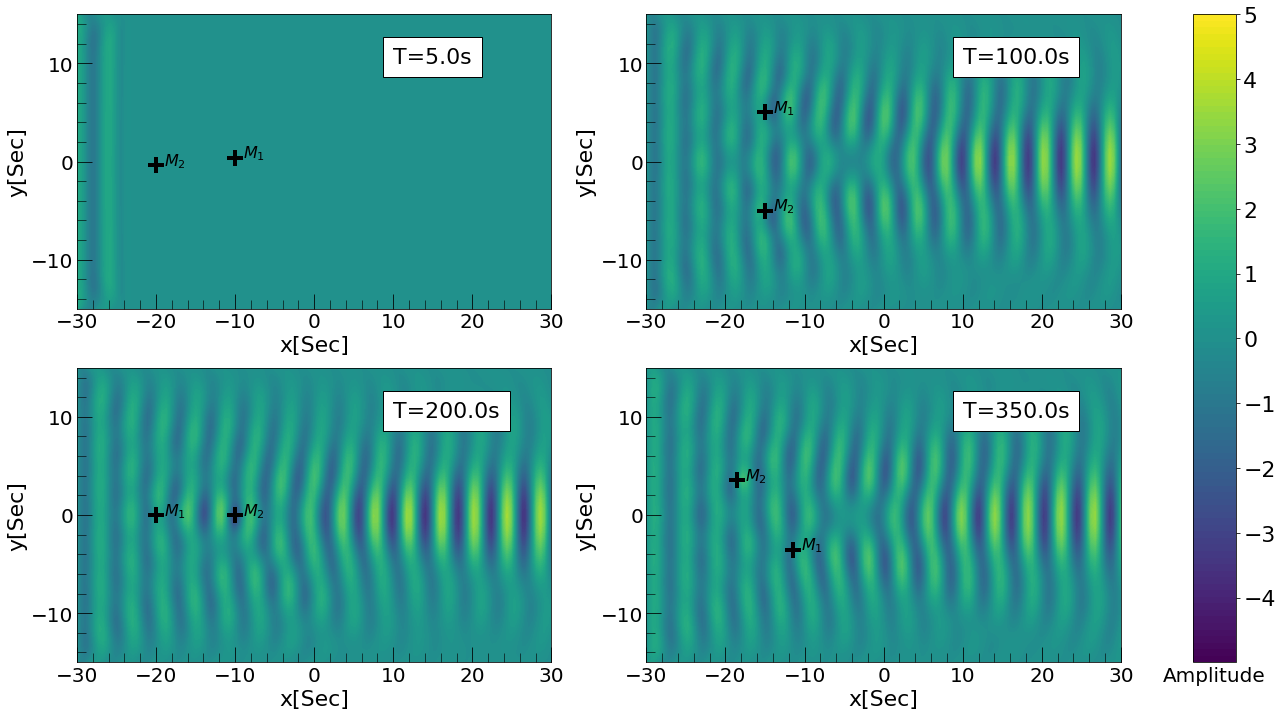
Amp_Spatial plot of our test case. The plot was done by taken a special slice at x-y plane (z=0) and the source GW is coming from the left.
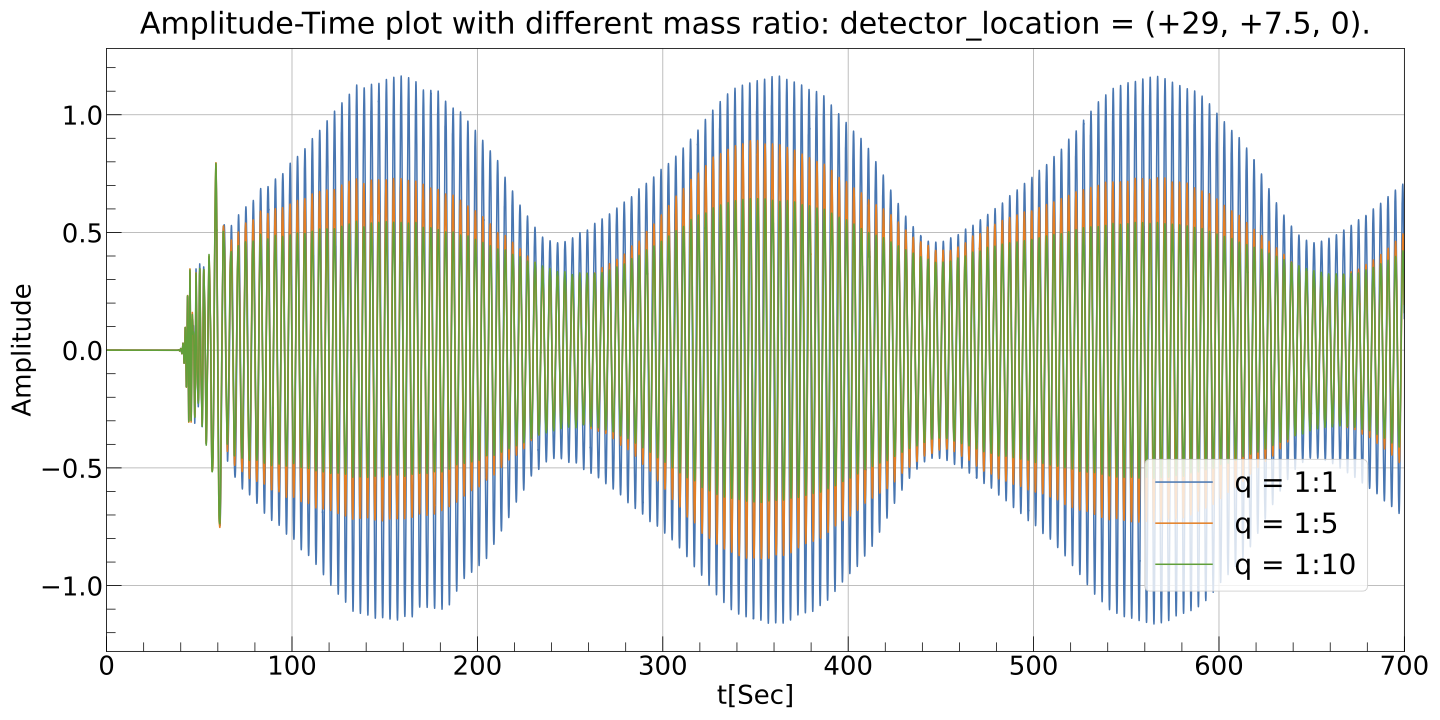
We ran our codes for (3/2 period + 5/3 box length) time of the spining BBH lensing system, which is 700 seconds. Here is one of the testcase:
Amp-T plot of ourgoing GWs with modulated waveform. The data was recorded at detector located ar one specific position.
FFT of the time-series data. (using the 1:1 mass ratio case)
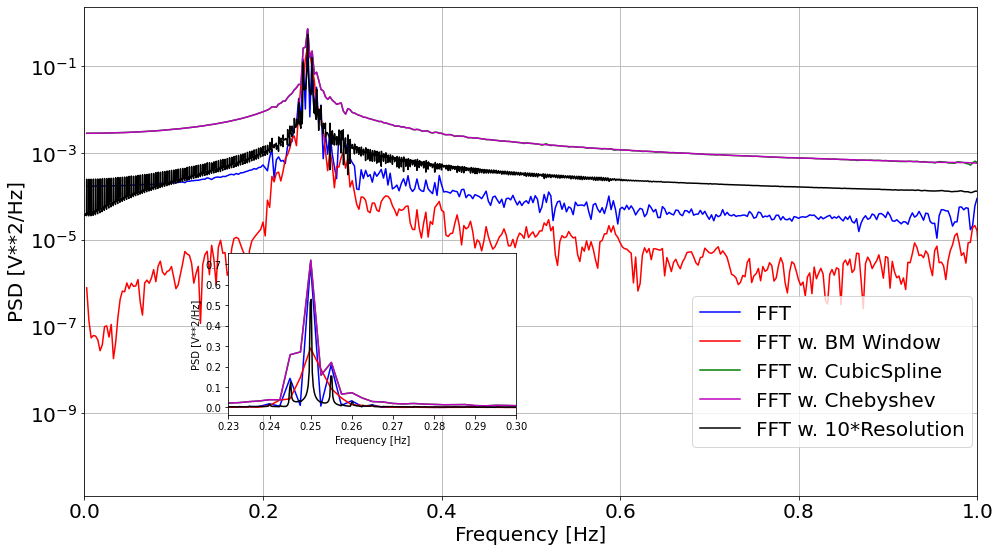
The higher frequency band becomes smoother as we interpolate the data (with both cubic order spline interpolation and Chebyshev polynomials interpolation), and the peak becomes sharper as we expand our cycle to 10*400s.
The number of peaks around source frequency (0.25Hz) was three, such pattern possibly represents a Fourier convolution of signals in the form of: \[ u(t)=\sin(2 \pi f_{source}t)\cdot[\alpha \sin(2\pi f_{binary}t)+\beta] \] Where the \(\alpha\) and \(\beta\) are coefficients depend on the distance between binaries, the polar angle toward which we detector the signal and mass ratio. Therefore, the above is the simplest form we might guess, while higher orders and some analytical derivation is also possible to make it more concrete and physically meaningful, which is what I am working on right now.
Reference
[1] He, Jian-Hua. “GWsim: A Code to Simulate Gravitational Waves Propagating in a Potential Well.” Monthly Notices of the Royal Astronomical Society 506, no. 4 (August 10, 2021): 5278–93. https://doi.org/10.1093/mnras/stab2080.