Chinese Undergraduate Innovation Training Program

Throughout my sophomore and junior years at Dalian University of Technology, I was the team leader of the innovation program "Application of machine learning in Quantum field theory". Me and my teammates worked with and advised by Prof. Weijie Fu and other graduate students in his group. We investigate how to use the machine learning methods for spectra function reconstruction. Below are the parts of work I mainly focused on.

• Breit-Wigner spectra function and its reconstruction

  In finite temperature QFT, we can get the spectra function from analytical continuation of imaginary time propagators since its form is quite simple under Euclidean metric. We used the Breit-Wigner propagator:

  \[ G(p_0)={A\over{(p_0+\Gamma)^2+M^2}} \] and corresponding spectra function:

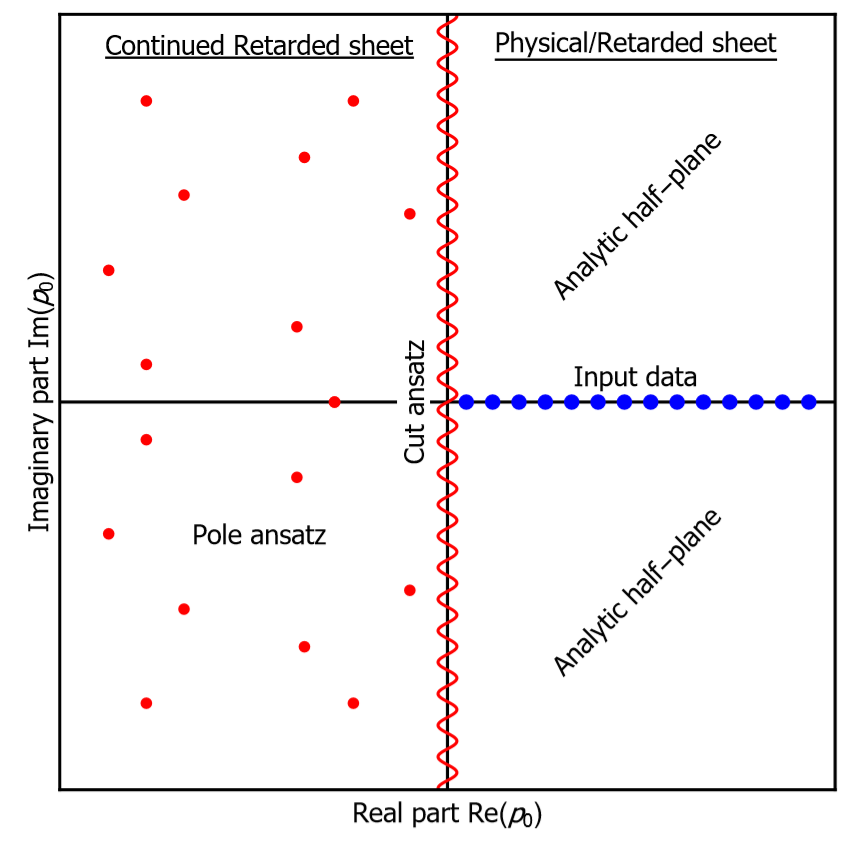
  \[ \rho(\omega)={4A\Gamma\omega\over{4\Gamma^2\omega ^2+(M^2+\Gamma^2-\omega^2)^2}} \] It can be seen from the picture (Analytic structure and singularities of propagator in complex plane, the image comes from \({Nicolas\space Wink}^{[1]}\)​) that we need to conclude the analytical structure and singularities of the propagator with a few discrete data points on the right half real plane to reconstruct the spectra function.

• Machine learning methods

  We established our training set by changing the position of the B-W propagators and the peak of the spectral functions. By using several different machine learning methods like BP neural network, CNN, GAN, adjusting the number of layers and batch size, and applying PCA (Principal Component Analysis) method, we have been successfully reconstruct B-W type spectra function with the supervised and unsupervised learning.

• Display of results

  These pictures below used 7 connected layers to reconstruct up to 2 peaks spectra function.

  

  The next step, we adopt the PCA with BatchNorm cases for dimension reduction and speed up the training process.

  

  We can find that the reconstruction results are still highly plausible.

In conclusion, machine learning method's advantage is that the reconstruction result is highly accurate, and once we have completed the network training, its calculation speed is unmatched by any previous method. The problem is that the supervised methods are Non-Bayesian, thus the error of the results is hard to accurately estimate. While, due to COVID-19, we failed to transform the project to a more formal research products, which is a great pity.

Reference

[1] Anton K Cyrol, Jan M Pawlowski, Alexander Rothkopf, and Nicolas Wink. Reconstructing the gluon. arXiv preprint arXiv:1804.00945, 2018.

[2] Rushil Anirudh, Jayaraman J Thiagarajan, Bhavya Kailkhura, and Timo Bremer. An Unsupervised Approach to Solving Inverse Problems using Generative Adversarial Networks. arXiv preprint arXiv: 1805.07281,2018.

[3] Yannis Burnier, Olaf Kaczmarek, and Alexander Rothkopf. The Bayesian reconstruction of the inmedium heavy quark potential from lattice QCD and its stability. In AIP Conference Proceedings, volume1701,page100017.AIPPublishing,2016.

[4] Yann LeCun, Yoshua Bengio, and Geoffrey Hinton. Deep learning. nature,521(7553):436, 2015.

[5] Y Nakahara, M Asakawa, and T Hatsuda. Hadronic spectral function sin lattice QCD. Physical Review D,60(9):091503, 1999.

[6] Alexander Rothkopf. Bayesian inference of nonpositive spectral functions in quantum field theory. Physical Review D,95(5):056016,2017.

[7] Ralf-Arno Tripolt, Philipp Gubler, Maksim Ulybyshev, and Lorenz von Smekal. Numerical analytic continuation of Euclidean data. arXiv preprint arXiv:1801.10348, 2018.